Construct and plot simplicial complexes that equal or approximate the topology of a ball cover of a set of points.
stat_simplicial_complex(
mapping = NULL,
data = NULL,
geom = "SimplicialComplex",
position = "identity",
complex = "Rips",
diameter = NULL,
radius = NULL,
dimension_max = 2L,
zero_simplices = "all",
one_simplices = "maximal",
engine = NULL,
na.rm = FALSE,
show.legend = NA,
inherit.aes = TRUE,
...
)
geom_simplicial_complex(
mapping = NULL,
data = NULL,
stat = "SimplicialComplex",
position = "identity",
outlines = TRUE,
na.rm = FALSE,
show.legend = NA,
inherit.aes = TRUE,
...
)Arguments
- mapping
Set of aesthetic mappings created by
aes(). If specified andinherit.aes = TRUE(the default), it is combined with the default mapping at the top level of the plot. You must supplymappingif there is no plot mapping.- data
The data to be displayed in this layer. There are three options:
If
NULL, the default, the data is inherited from the plot data as specified in the call toggplot().A
data.frame, or other object, will override the plot data. All objects will be fortified to produce a data frame. Seefortify()for which variables will be created.A
functionwill be called with a single argument, the plot data. The return value must be adata.frame, and will be used as the layer data. Afunctioncan be created from aformula(e.g.~ head(.x, 10)).- geom
The geometric object to use to display the data, either as a
ggprotoGeomsubclass or as a string naming the geom stripped of thegeom_prefix (e.g."point"rather than"geom_point")- position
Position adjustment, either as a string naming the adjustment (e.g.
"jitter"to useposition_jitter), or the result of a call to a position adjustment function. Use the latter if you need to change the settings of the adjustment.- complex
The type of complex to compute, one of
"Vietoris","Rips"(equivalent),"Cech", or"alpha".- radius, diameter
The (positive) radius or diameter used in the construction. Provide only one of these; if neither is provided, they default to zero.
- dimension_max
Compute simplices of dimension up to
dimension_max(only relevant for the Vietoris--Rips complex computed with thesimplextreeengine).- zero_simplices
Which 0-simplices (vertices) to plot; one of
"none","maximal", and"all"(default).- one_simplices
Which 1-simplices (edges) to plot; one of
"none","maximal"(default), and"all".- engine
The computational engine to use (see 'Details'). Reasonable defaults are chosen based on
complex.- na.rm
If
FALSE, the default, missing values are removed with a warning. IfTRUE, missing values are silently removed.- show.legend
logical. Should this layer be included in the legends?
NA, the default, includes if any aesthetics are mapped.FALSEnever includes, andTRUEalways includes. It can also be a named logical vector to finely select the aesthetics to display.- inherit.aes
If
FALSE, overrides the default aesthetics, rather than combining with them. This is most useful for helper functions that define both data and aesthetics and shouldn't inherit behaviour from the default plot specification, e.g.borders().- ...
Other arguments passed on to
layer(). These are often aesthetics, used to set an aesthetic to a fixed value, likecolour = "red"orsize = 3. They may also be parameters to the paired geom/stat.- stat
The statistical transformation to use on the data for this layer, either as a
ggprotoGeomsubclass or as a string naming the stat stripped of thestat_prefix (e.g."count"rather than"stat_count")- outlines
Should the outlines of polygons representing high-dimensional simplices be drawn?
Details
Persistent homology is ultimately based on the topological properties of regions containing a set of points. When the region is the union of balls of a common radius, its homology is equal to or approximated by that of several families of simplicial complexes constructed on the point set. The simplicial complex stat constructs these simplicial complexes for a set of points in \(xy\)-space while the geom plots them on the same coordinates as the points.
Complexes
A Vietoris--Rips complex of a point cloud is the simplicial complex consisting of a simplex for each subset of points within a fixed diameter of each other. A Čech complex contains the simplex for each subset that lies within a circle of fixed diameter. (This means that the Čech complex depends on the geometry of the ambient space containing the point cloud, while the Vietoris complex depends only on the inter-point distances. Moreover, a Vietoris complex contains the Čech complex of the same diameter.) An alpha complex comprises those simplices of the Delaunay triangulation within a fixed diameter.
ggtda relies on four engines to compute simplicial complexes, which
can be specified to the engine parameter: Vietoris--Rips and Čech
complexes of dimension at most 2 are implemented in base R ("base"),
which is slow but allows the package to stand alone for small cases.
RTriangle::triangulate() is used to compute the Delaunay triangulation
for alpha complexes ("RTriangle"), without inserting Steiner points (so
that the vertices of the triangulation are among those of the data). The
package TDA can compute Vietoris--Rips filtrations and alpha filtrations ("TDA" for default engines,
or specify the "GUDHI" or "Dionysus" engine). Finally, the highly
optimized package
simplextree can be called
to compute Vietoris--Rips complexes ("simplextree"). As other complexes
are implemented in simplextree, they will be made available here.
Aesthetics
stat_simplicial_complex() understands the following aesthetics (required aesthetics are in bold):
xygroup
geom_simplicial_complex() understands the following aesthetics (required aesthetics are in bold):
xyiddimensionalphacolourfillgrouplinetypelinewidthshapesizestroke
Learn more about setting these aesthetics in vignette("ggplot2-specs", package = "ggplot2").
Computed variables
stat_simplicial_complex calculates the following variables that can be accessed with delayed evaluation.
after_stat(dimension)
integer dimension of the corresponding simplex.after_stat(id)
character simplex identifier within eachdimension.after_stat(face)
factor encoding ofdimensionfor>= 2L-dimensional simplices.
See also
ggplot2::layer() for additional arguments.
Other plot layers for point clouds:
disk
Examples
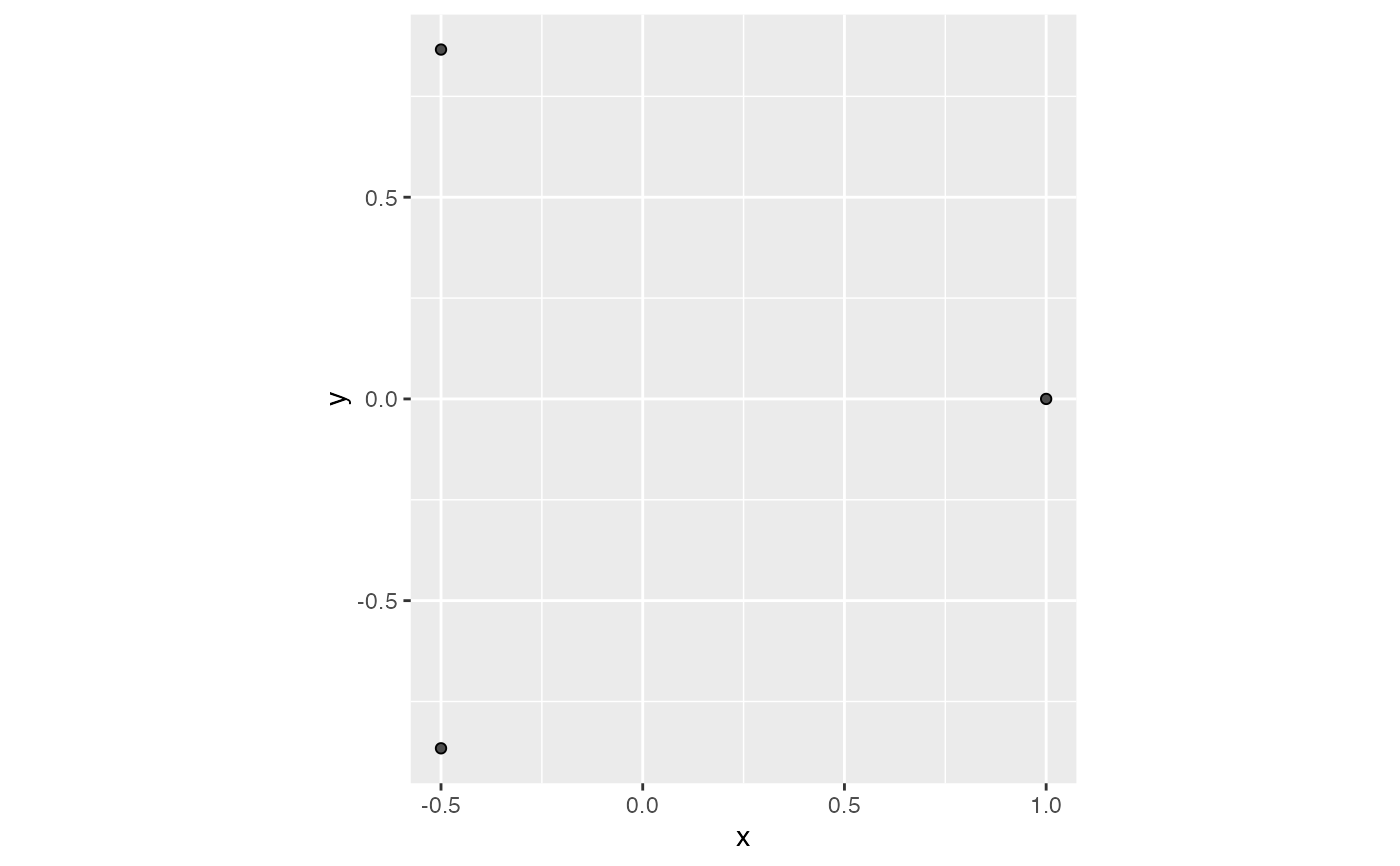
# equilateral triangle
equilateral_triangle <-
data.frame(x = cos(2*pi*c(0,1/3,2/3)), y = sin(2*pi*c(0,1/3,2/3)))
# small perturbations from key values
eps <- .00000001
# Vietoris-Rips
ggplot(equilateral_triangle, aes(x, y)) +
coord_fixed() +
geom_simplicial_complex(diameter = sqrt(3) - eps)
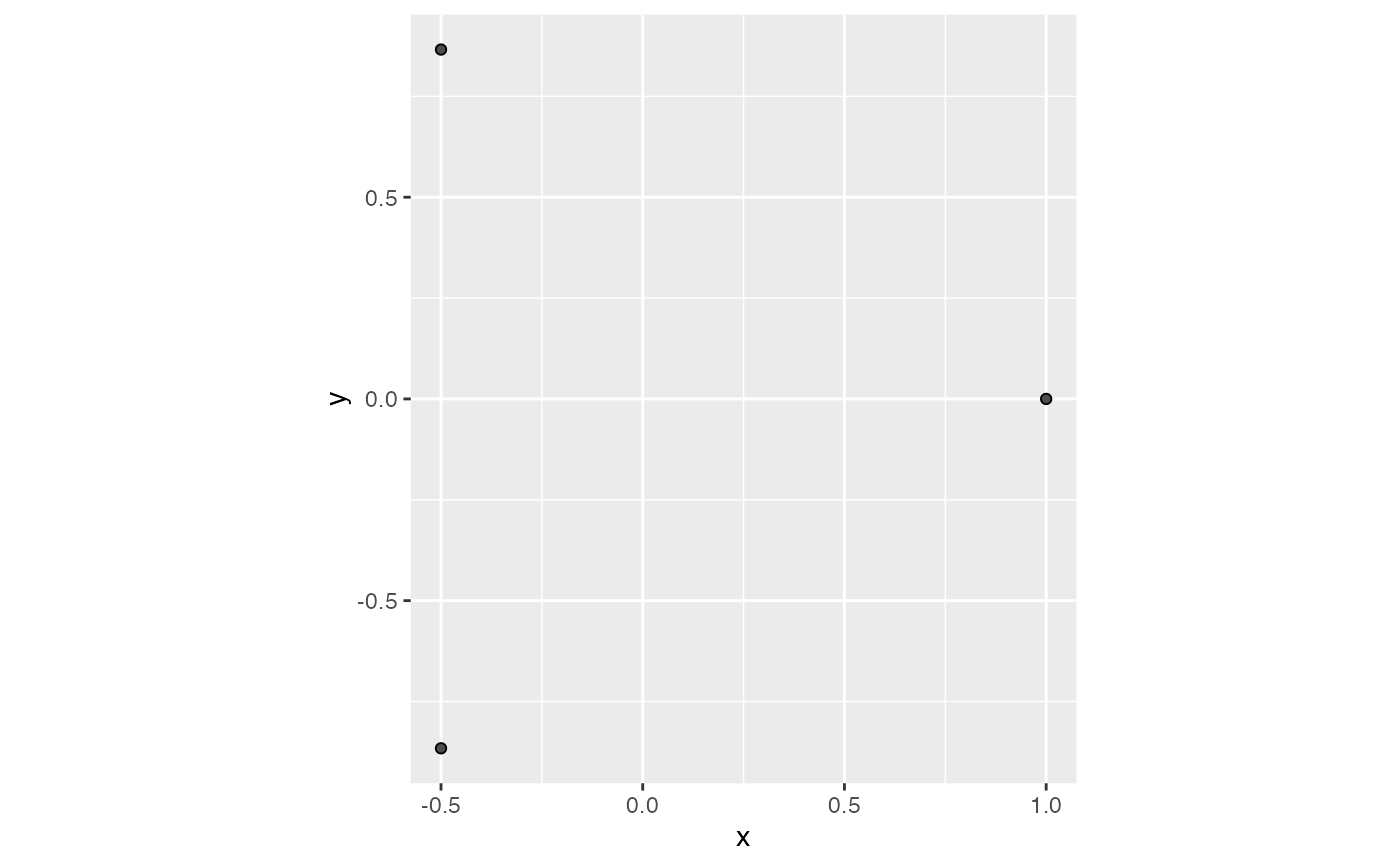 ggplot(equilateral_triangle, aes(x, y)) +
coord_fixed() +
geom_simplicial_complex(diameter = sqrt(3) + eps)
ggplot(equilateral_triangle, aes(x, y)) +
coord_fixed() +
geom_simplicial_complex(diameter = sqrt(3) + eps)
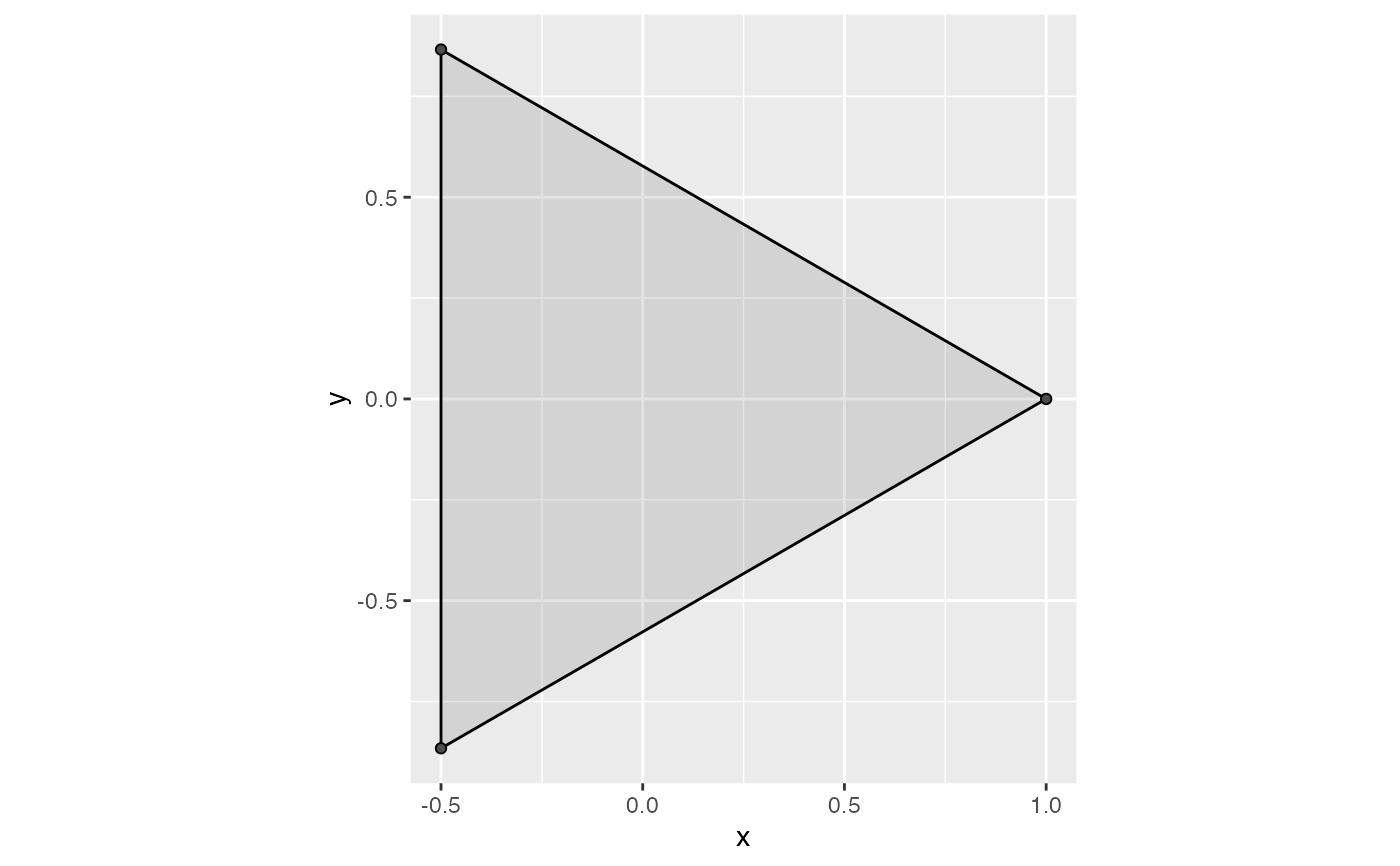 # Čech
ggplot(equilateral_triangle, aes(x, y)) +
coord_fixed() +
geom_simplicial_complex(complex = "Cech", diameter = sqrt(3) - eps)
# Čech
ggplot(equilateral_triangle, aes(x, y)) +
coord_fixed() +
geom_simplicial_complex(complex = "Cech", diameter = sqrt(3) - eps)
 ggplot(equilateral_triangle, aes(x, y)) +
coord_fixed() +
geom_simplicial_complex(complex = "Cech", diameter = sqrt(3) + eps)
ggplot(equilateral_triangle, aes(x, y)) +
coord_fixed() +
geom_simplicial_complex(complex = "Cech", diameter = sqrt(3) + eps)
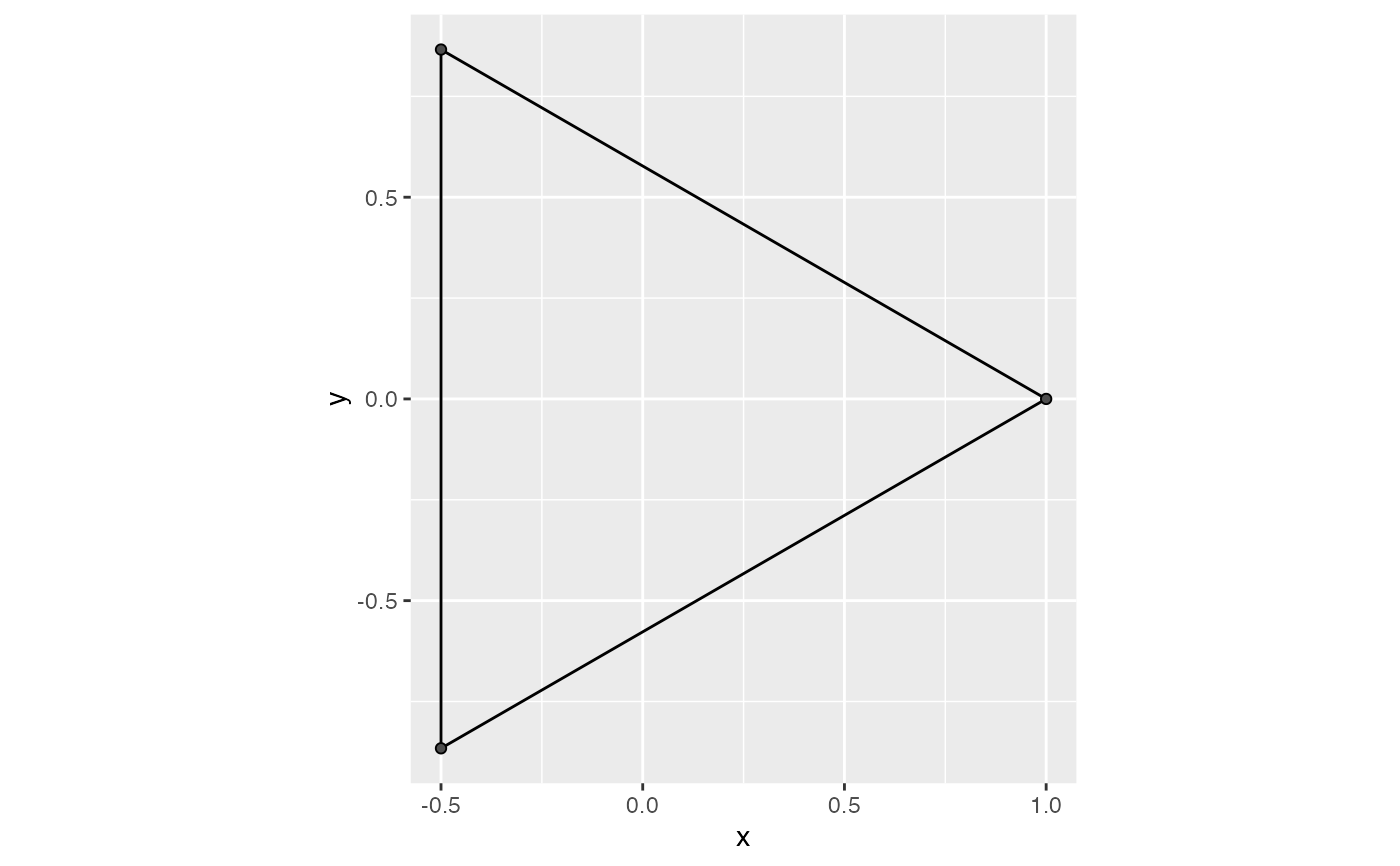 # alpha
ggplot(equilateral_triangle, aes(x, y)) +
coord_fixed() +
geom_simplicial_complex(complex = "alpha", diameter = sqrt(3) - eps)
# alpha
ggplot(equilateral_triangle, aes(x, y)) +
coord_fixed() +
geom_simplicial_complex(complex = "alpha", diameter = sqrt(3) - eps)
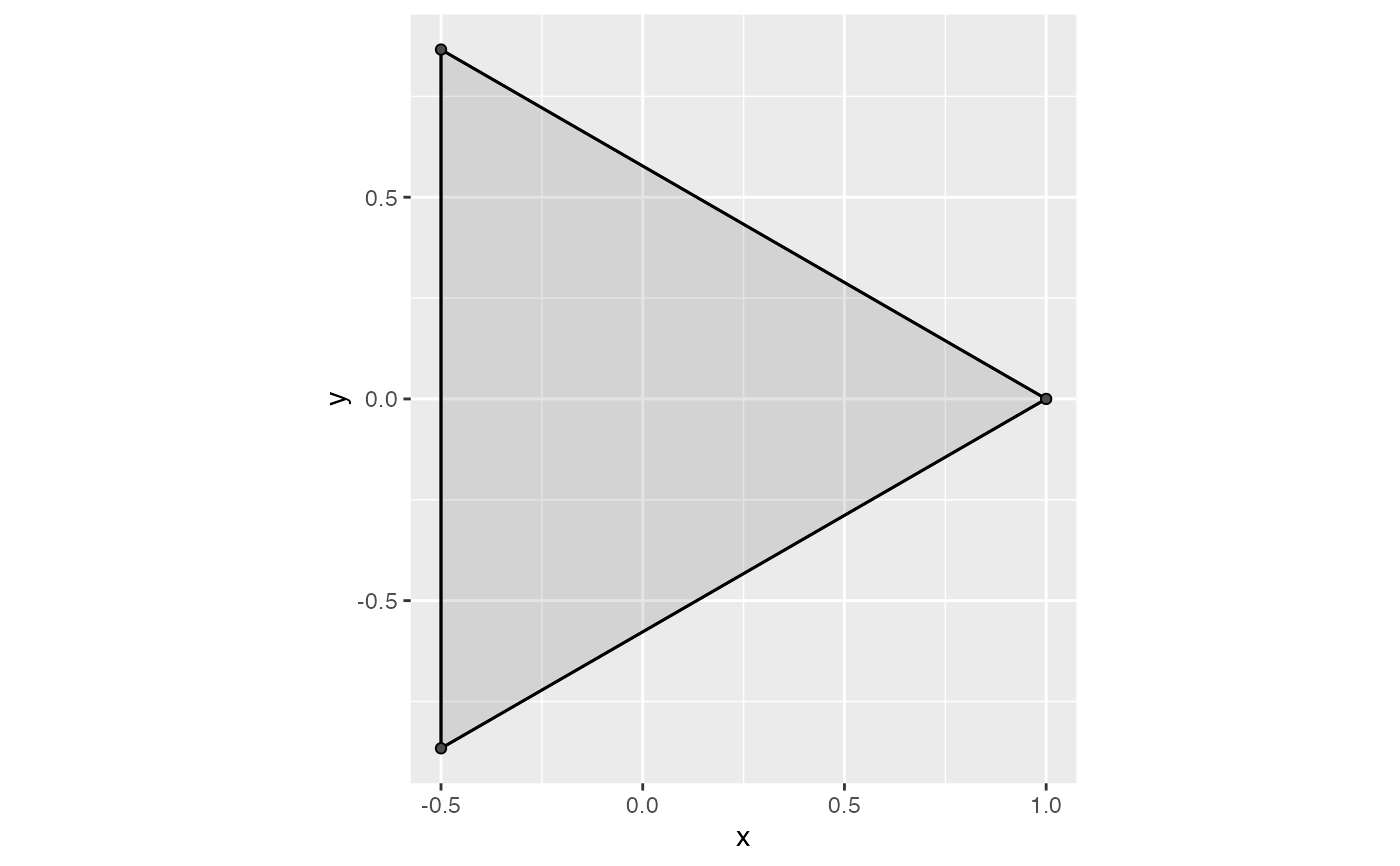 ggplot(equilateral_triangle, aes(x, y)) +
coord_fixed() +
geom_simplicial_complex(complex = "alpha", diameter = sqrt(3) + eps)
ggplot(equilateral_triangle, aes(x, y)) +
coord_fixed() +
geom_simplicial_complex(complex = "alpha", diameter = sqrt(3) + eps)
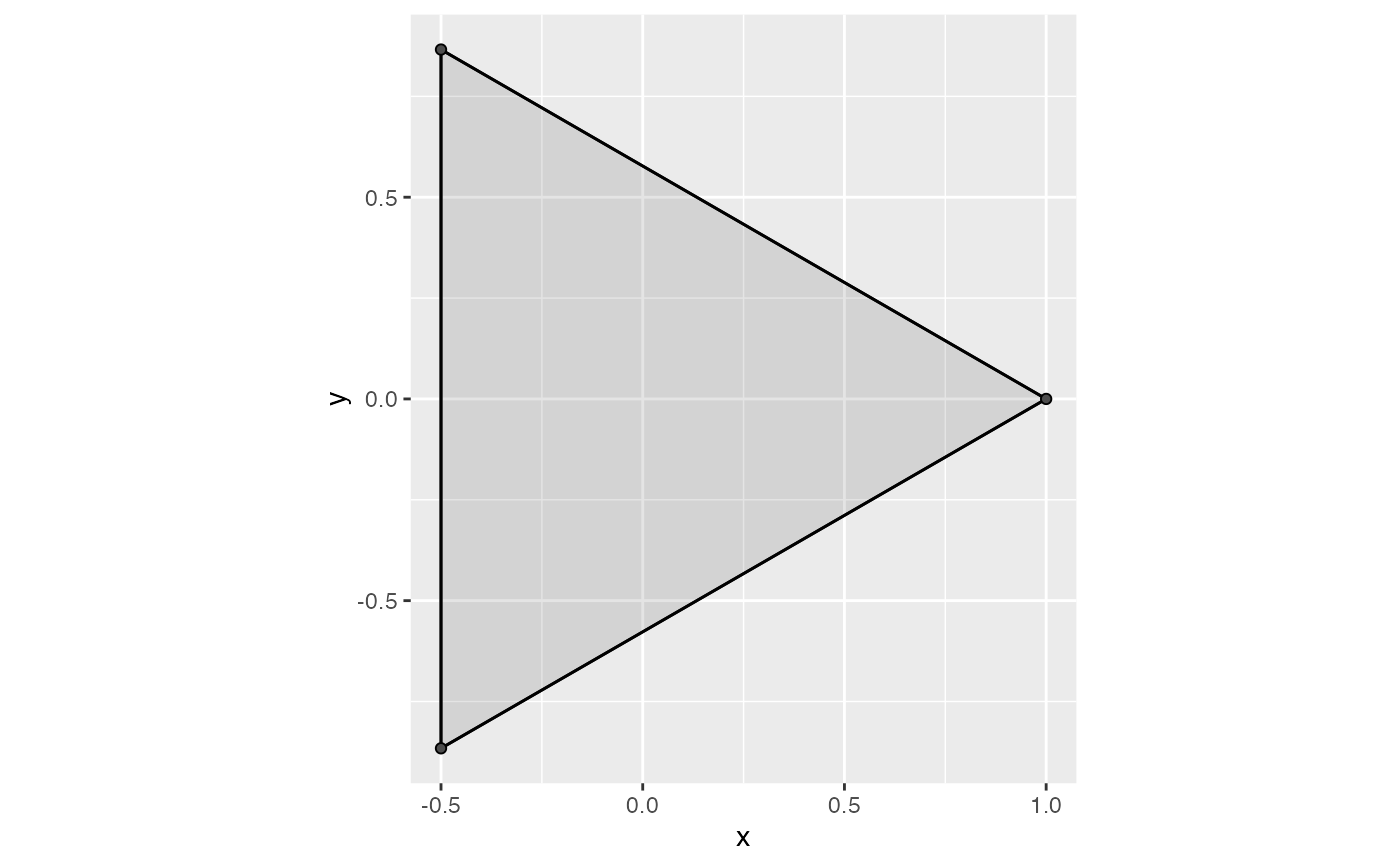 set.seed(1)
s <- seq(0, 2*pi, length.out = 40)
df <- data.frame(
x = cos(s) + rnorm(40, 0, .1),
y = sin(s) + rnorm(40, 0, .1)
)
# default
ggplot(df, aes(x, y)) +
coord_fixed() +
geom_simplicial_complex(radius = .4)
set.seed(1)
s <- seq(0, 2*pi, length.out = 40)
df <- data.frame(
x = cos(s) + rnorm(40, 0, .1),
y = sin(s) + rnorm(40, 0, .1)
)
# default
ggplot(df, aes(x, y)) +
coord_fixed() +
geom_simplicial_complex(radius = .4)
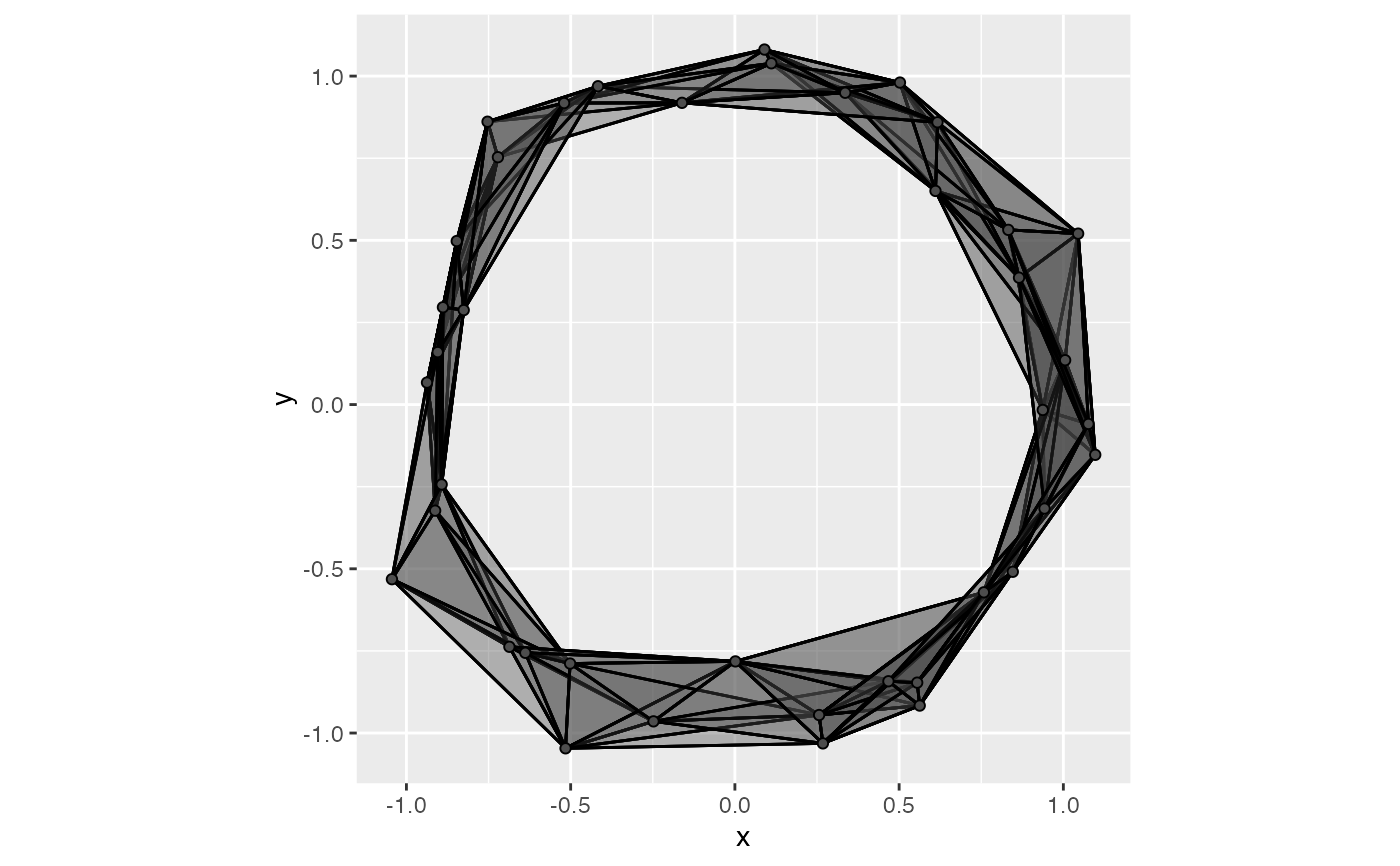 # higher-dimensional simplices are not more opaque but cause overlap
ggplot(df, aes(x, y)) +
coord_fixed() +
geom_simplicial_complex(radius = .4, dimension_max = 3L)
# higher-dimensional simplices are not more opaque but cause overlap
ggplot(df, aes(x, y)) +
coord_fixed() +
geom_simplicial_complex(radius = .4, dimension_max = 3L)
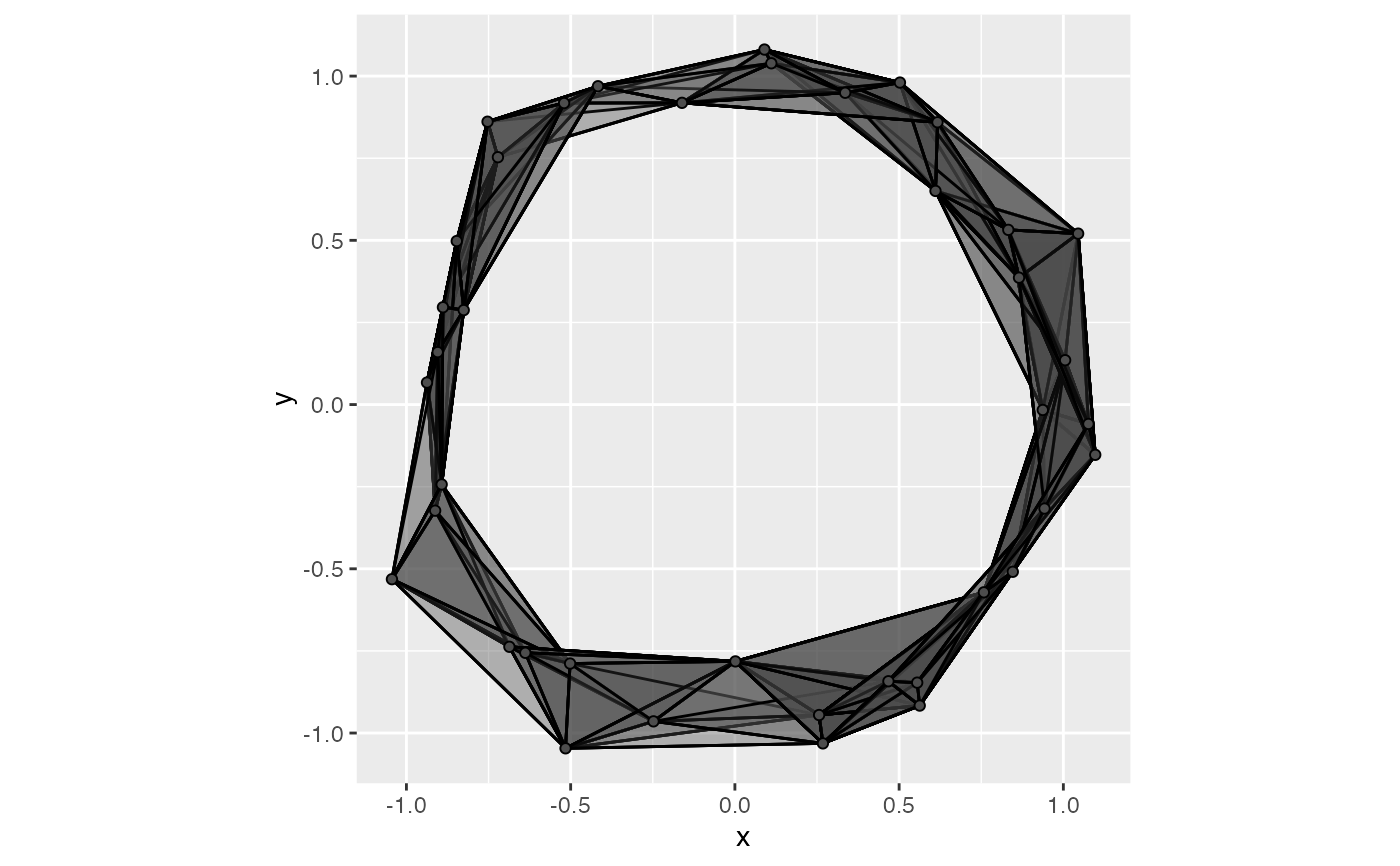 # visualizing dimension w/ face & alpha:
ggplot(df, aes(x, y)) +
coord_fixed() +
geom_simplicial_complex(
mapping = aes(alpha = after_stat(face)),
radius = .3, dimension_max = 4L
) +
scale_alpha_ordinal(range = c(.1, .6))
# visualizing dimension w/ face & alpha:
ggplot(df, aes(x, y)) +
coord_fixed() +
geom_simplicial_complex(
mapping = aes(alpha = after_stat(face)),
radius = .3, dimension_max = 4L
) +
scale_alpha_ordinal(range = c(.1, .6))
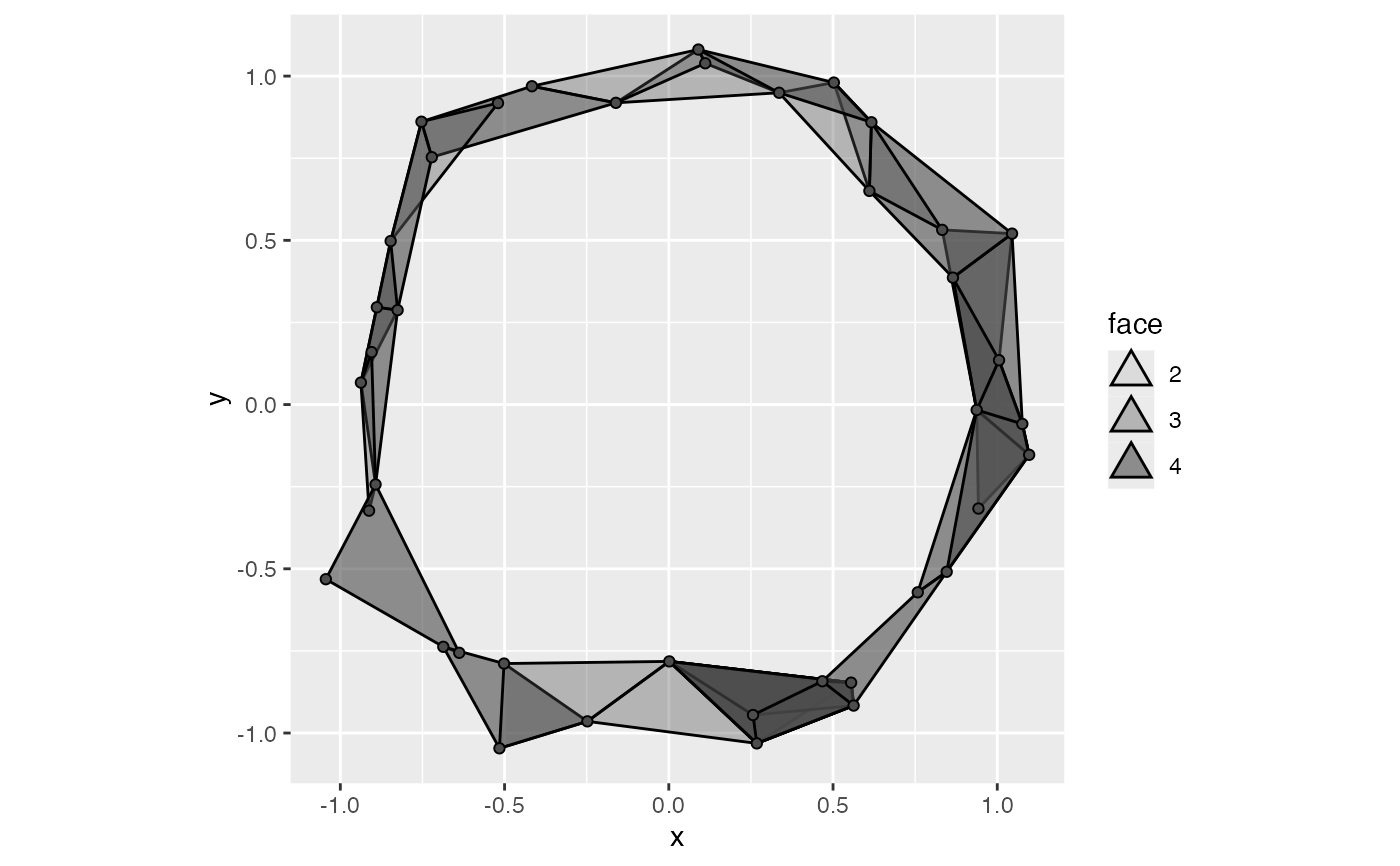 # visualizing dimension w/ dimension & fill:
ggplot(df, aes(x, y)) +
coord_fixed() +
geom_simplicial_complex(
mapping = aes(fill = after_stat(dimension)),
radius = .3, dimension_max = 4L, alpha = .25
) +
scale_fill_continuous(type = "viridis")
# visualizing dimension w/ dimension & fill:
ggplot(df, aes(x, y)) +
coord_fixed() +
geom_simplicial_complex(
mapping = aes(fill = after_stat(dimension)),
radius = .3, dimension_max = 4L, alpha = .25
) +
scale_fill_continuous(type = "viridis")
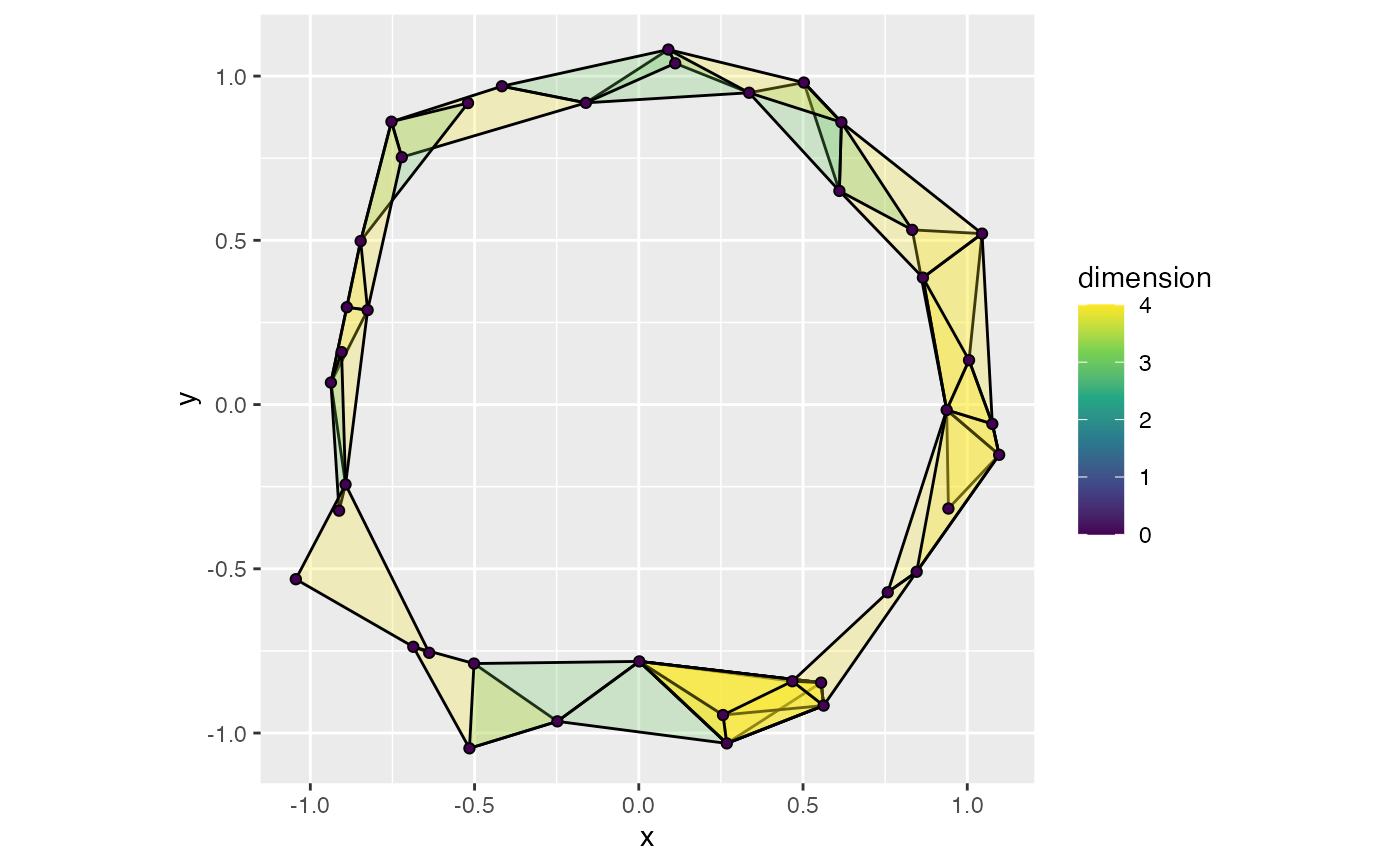 # with a zero radius or diameter
ggplot(df, aes(x = x, y = y)) +
coord_fixed() +
stat_simplicial_complex(radius = 0)
# with a zero radius or diameter
ggplot(df, aes(x = x, y = y)) +
coord_fixed() +
stat_simplicial_complex(radius = 0)
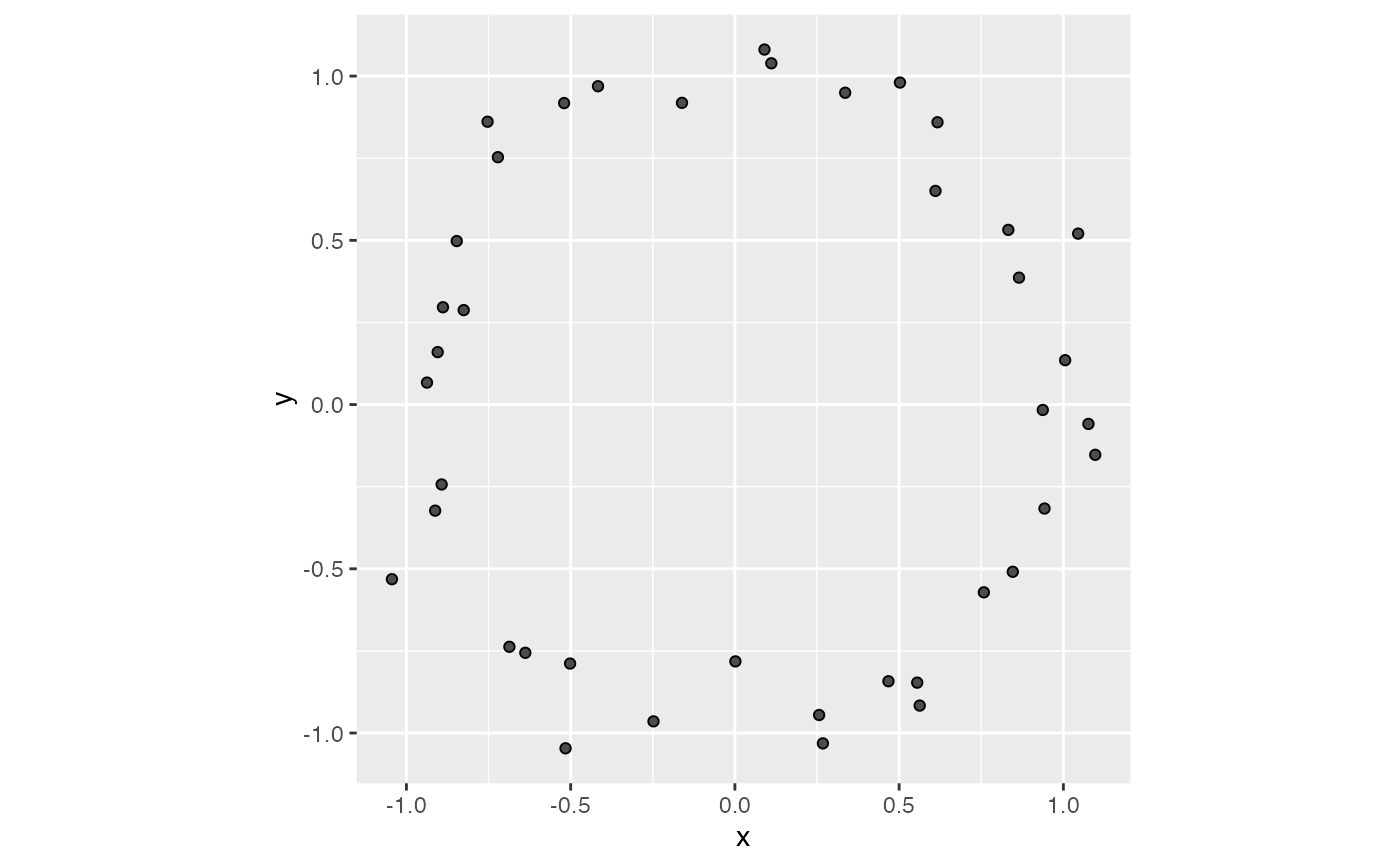 # with a too-small radius or diameter
ggplot(df, aes(x = x, y = y)) +
coord_fixed() +
stat_simplicial_complex(radius = 0.01)
# with a too-small radius or diameter
ggplot(df, aes(x = x, y = y)) +
coord_fixed() +
stat_simplicial_complex(radius = 0.01)
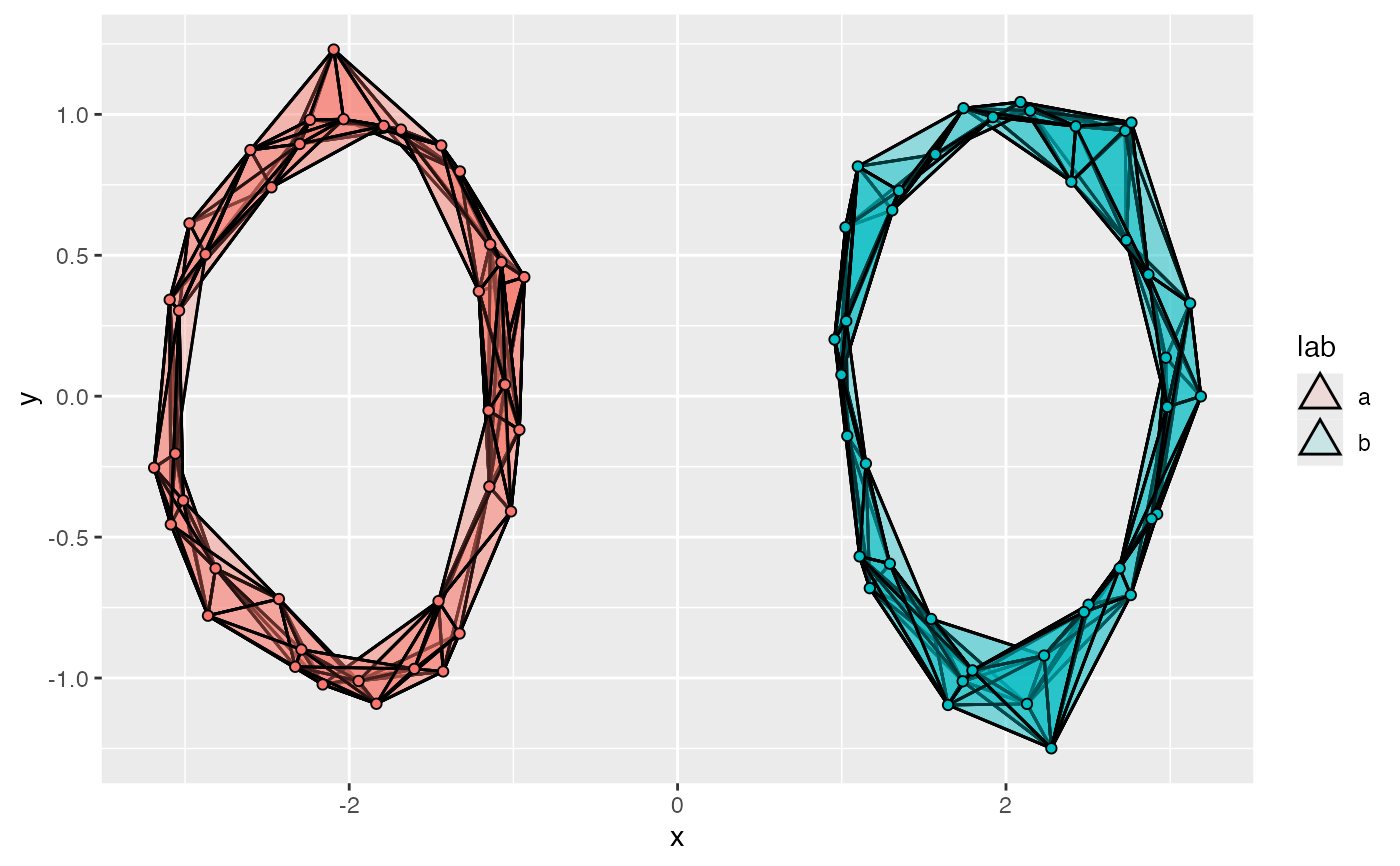
 # Visualizing multiple groups together
s <- c(s, s)
df_mix <- data.frame(
x = cos(s) + rnorm(80, 0, .1),
y = sin(s) + rnorm(80, 0, .1)
)
df_mix$x <- df_mix$x + rep(c(-2, 2), length.out = 80)
df_mix$lab <- rep(c("a", "b"), length.out = 80)
ggplot(df_mix, aes(x, y, fill = lab)) +
geom_simplicial_complex(radius = .4)
# Visualizing multiple groups together
s <- c(s, s)
df_mix <- data.frame(
x = cos(s) + rnorm(80, 0, .1),
y = sin(s) + rnorm(80, 0, .1)
)
df_mix$x <- df_mix$x + rep(c(-2, 2), length.out = 80)
df_mix$lab <- rep(c("a", "b"), length.out = 80)
ggplot(df_mix, aes(x, y, fill = lab)) +
geom_simplicial_complex(radius = .4)
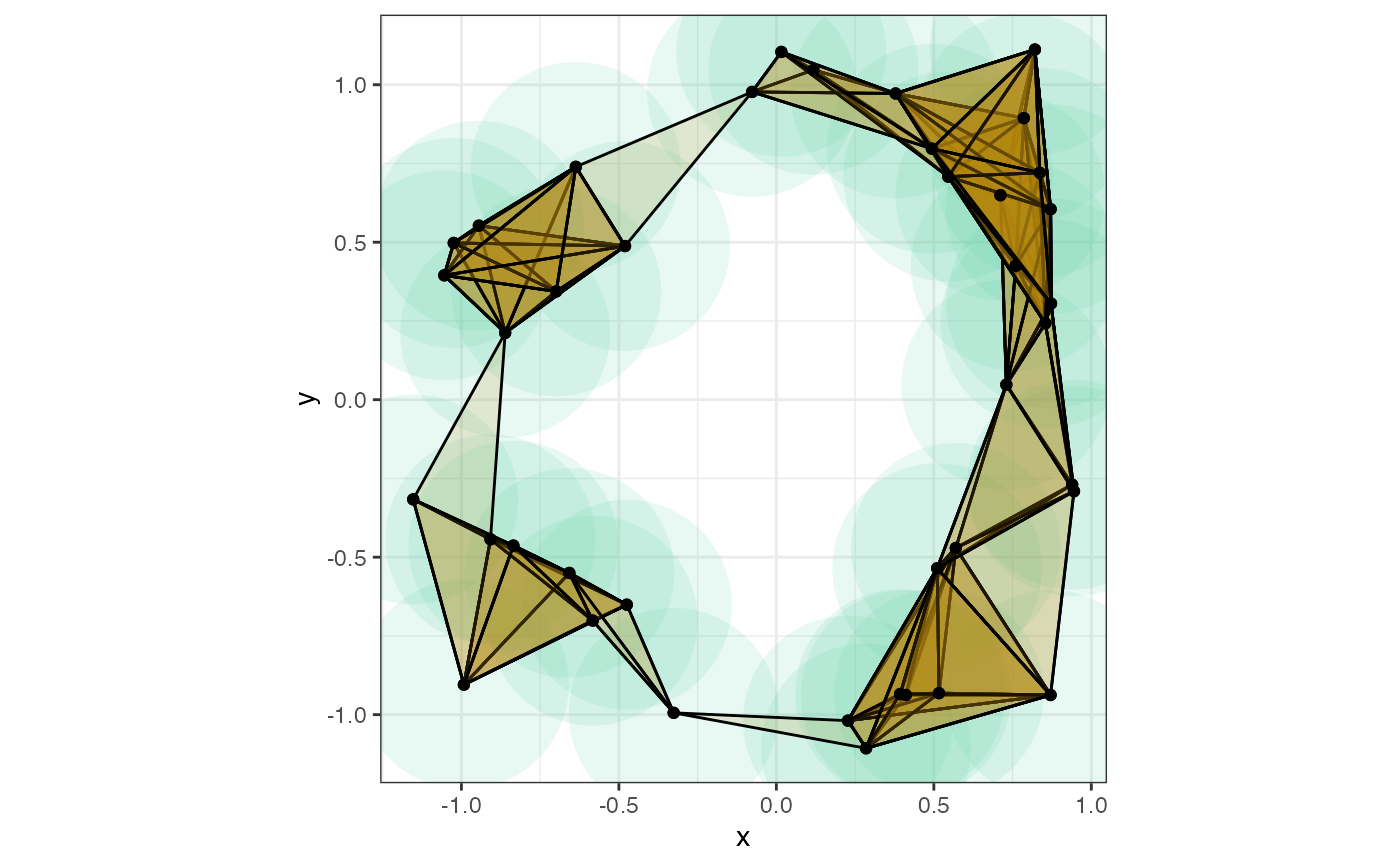
 # generate a noisy 2D circle
set.seed(2)
theta <- stats::runif(n = 40L, min = 0, max = 2*pi)
d <- data.frame(x = cos(theta) + stats::rnorm(40L, 0, .15),
y = sin(theta) + stats::rnorm(40L, 0, .15))
r <- 1/3
# overlay ball cover and Vietoris-Rips complex with points
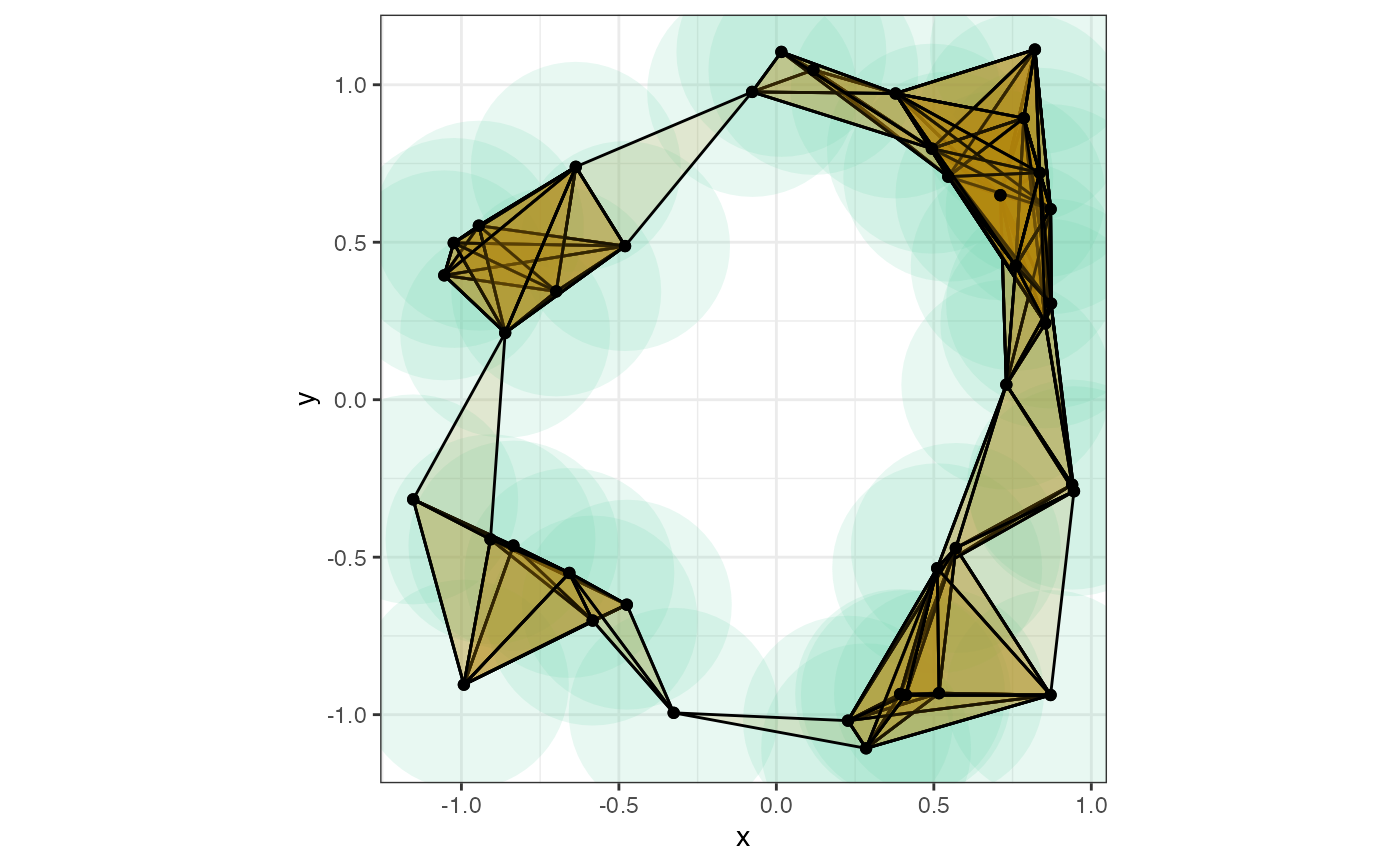
ggplot(d, aes(x = x, y = y)) +
theme_bw() +
coord_fixed() +
geom_disk(radius = r, fill = "aquamarine3") +
geom_simplicial_complex(
radius = r, fill = "darkgoldenrod",
complex = "Vietoris", engine = "base"
) +
geom_point()
# generate a noisy 2D circle
set.seed(2)
theta <- stats::runif(n = 40L, min = 0, max = 2*pi)
d <- data.frame(x = cos(theta) + stats::rnorm(40L, 0, .15),
y = sin(theta) + stats::rnorm(40L, 0, .15))
r <- 1/3
# overlay ball cover and Vietoris-Rips complex with points
ggplot(d, aes(x = x, y = y)) +
theme_bw() +
coord_fixed() +
geom_disk(radius = r, fill = "aquamarine3") +
geom_simplicial_complex(
radius = r, fill = "darkgoldenrod",
complex = "Vietoris", engine = "base"
) +
geom_point()
 # use the Čech complex instead
ggplot(d, aes(x = x, y = y)) +
theme_bw() +
coord_fixed() +
geom_disk(radius = r, fill = "aquamarine3") +
geom_simplicial_complex(
radius = r, fill = "darkgoldenrod",
complex = "Cech", engine = "base"
) +
geom_point()
# use the Čech complex instead
ggplot(d, aes(x = x, y = y)) +
theme_bw() +
coord_fixed() +
geom_disk(radius = r, fill = "aquamarine3") +
geom_simplicial_complex(
radius = r, fill = "darkgoldenrod",
complex = "Cech", engine = "base"
) +
geom_point()