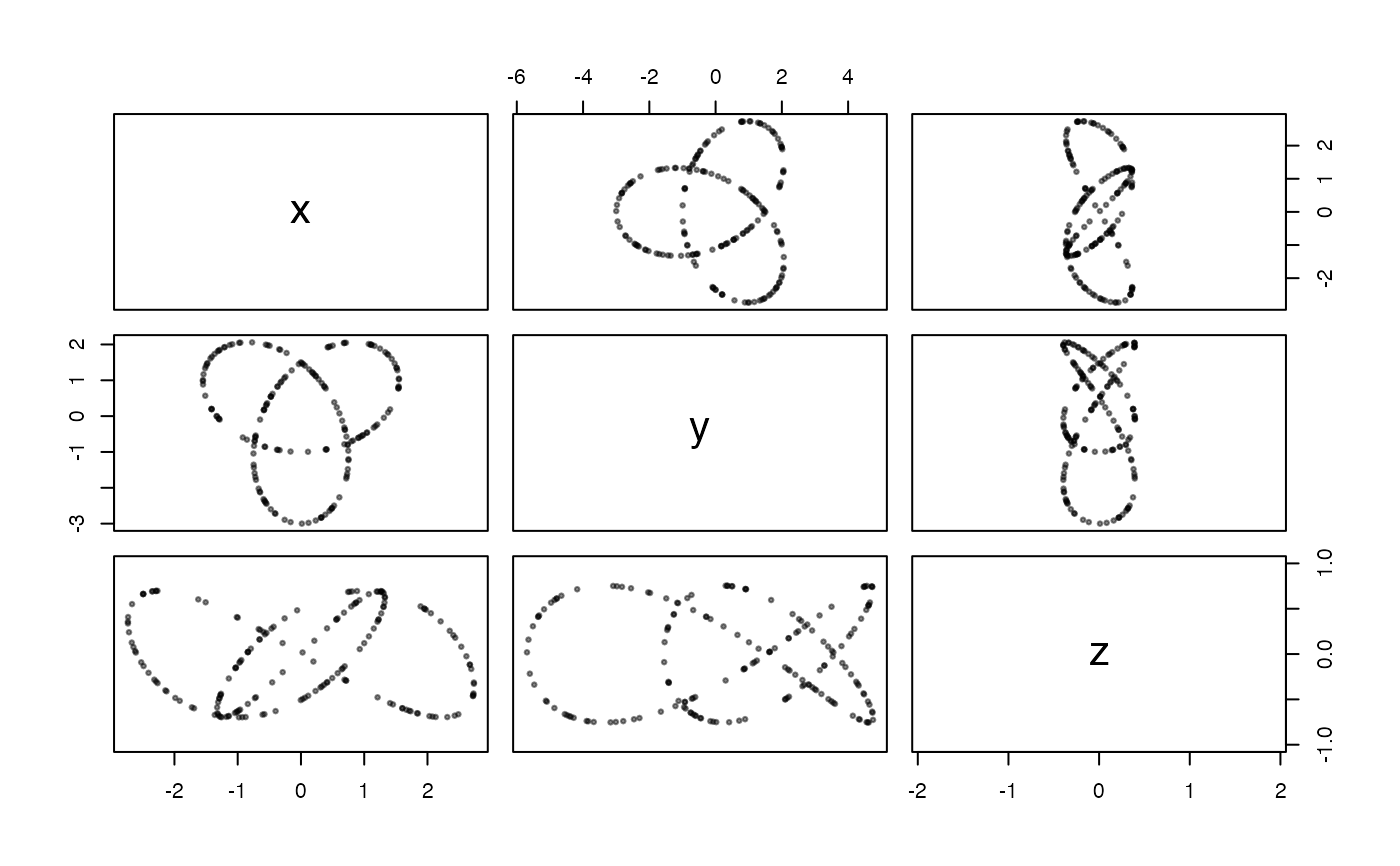
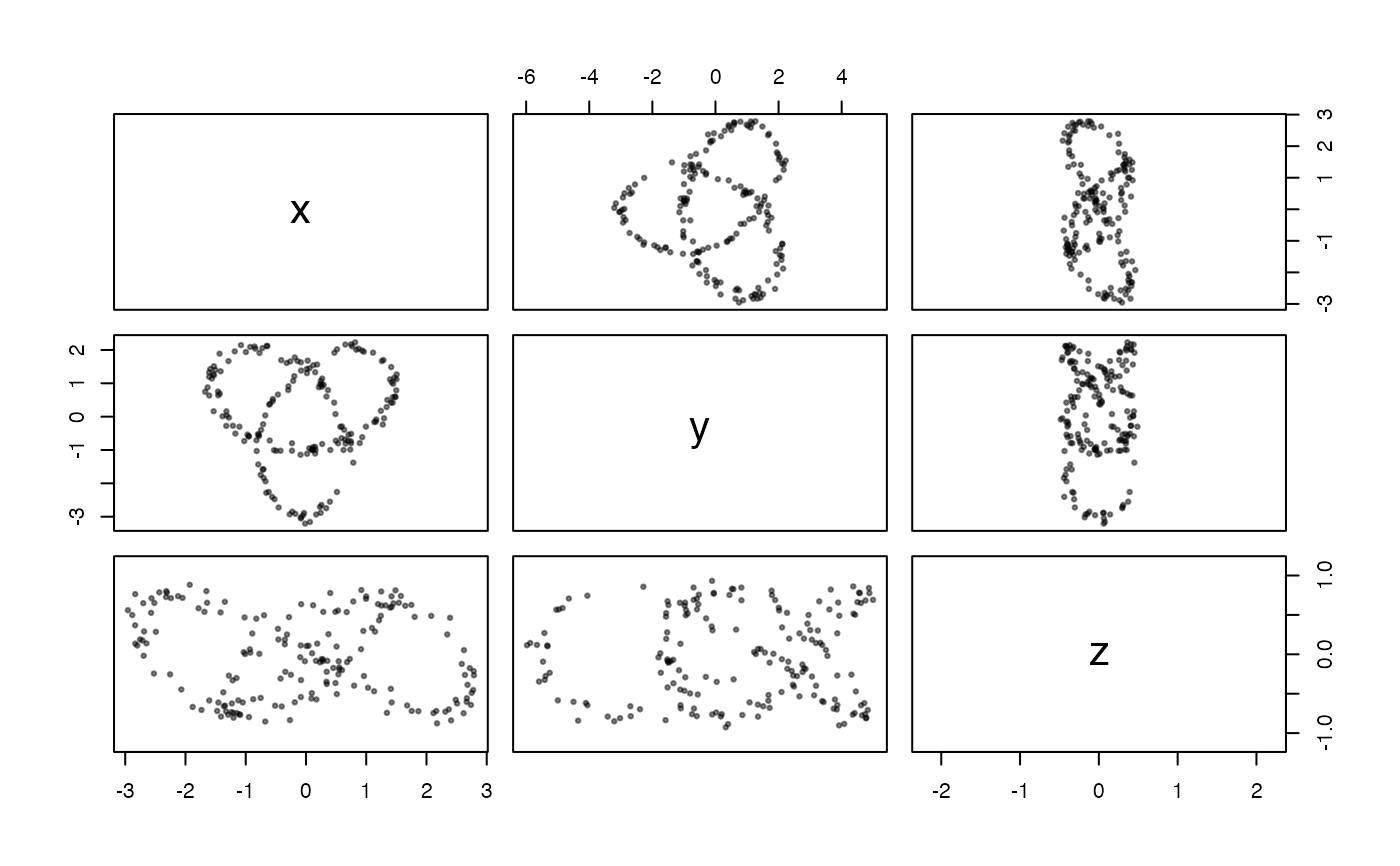
Sample (with noise) from trefoil knot

Source: R/trefoil.r

These functions generate uniform samples from trefoil knot in 3-dimensional space, optionally with noise.

sample_trefoil(n, sd = 0)

Arguments

n

Number of observations.

sd

Standard deviation of (independent multivariate) Gaussian noise.

Details

The trefoil knot is the simplest nontrivial knot and contains three unique crossings in three dimensional space. This uniform sample is generated by rejection sampling. This process allows for simulation of random samples from the trefoil knot distribution, by using random samples from a more convenient distribution. It applies rejection/acceptance criterion such that the samples that are accepted are to be distributed as if they were from the target distribution. The uniform sample is generated through a rejection sampling process as described by Diaconis, Holmes, and Shahshahani (2013).

References

P Diaconis, S Holmes, and M Shahshahani (2013) Sampling from a Manifold. Advances in Modern Statistical Theory and Applications: A Festschrift in honor of Morris L. Eaton, 102--125. doi:10.1214/12-IMSCOLL1006

Examples

set.seed(73398L)

# Uniformly sampled trefoil knot in 3-space
x <- sample_trefoil(180)
pairs(x, asp = 1, pch = 19, cex = .5, col = "#00000077")


# Uniformly sampled trefoil knot in 3-space, with Gaussian noise
x <- sample_trefoil(180, sd = .1)
pairs(x, asp = 1, pch = 19, cex = .5, col = "#00000077")