These functions generate uniform samples from configurations of tori of primary radius 1 in 3-dimensional space, optionally with noise.
sample_torus_tube(n, ar = 2, sd = 0)
sample_tori_interlocked(n, ar = 2, sd = 0)
sample_torus_flat(n, ar = 1, sd = 0)Arguments
- n
Number of observations.
- ar
Aspect ratio for tube torus (ratio of major and minor radii) or flat torus (ratio of scale factors).
- sd
Standard deviation of (independent multivariate) Gaussian noise.
Details
The function sample_torus_tube() uses the tubular parameterization into
3-dimensional space documented at
MathWorld.
The function sample_torus_flat() uses a flat parameterization (having zero
Gaussian curvature) into 4-dimensional space, as presented on
Wikipedia.
The function sample_tori_interlocked() samples from two tubular tori
interlocked in the same way as sample_circles_interlocked().
All uniform samples are generated through a rejection sampling process as described by Diaconis, Holmes, and Shahshahani (2013).
References
P Diaconis, S Holmes, and M Shahshahani (2013) Sampling from a Manifold. Advances in Modern Statistical Theory and Applications: A Festschrift in honor of Morris L. Eaton, 102--125. doi:10.1214/12-IMSCOLL1006
Examples
set.seed(33183L)
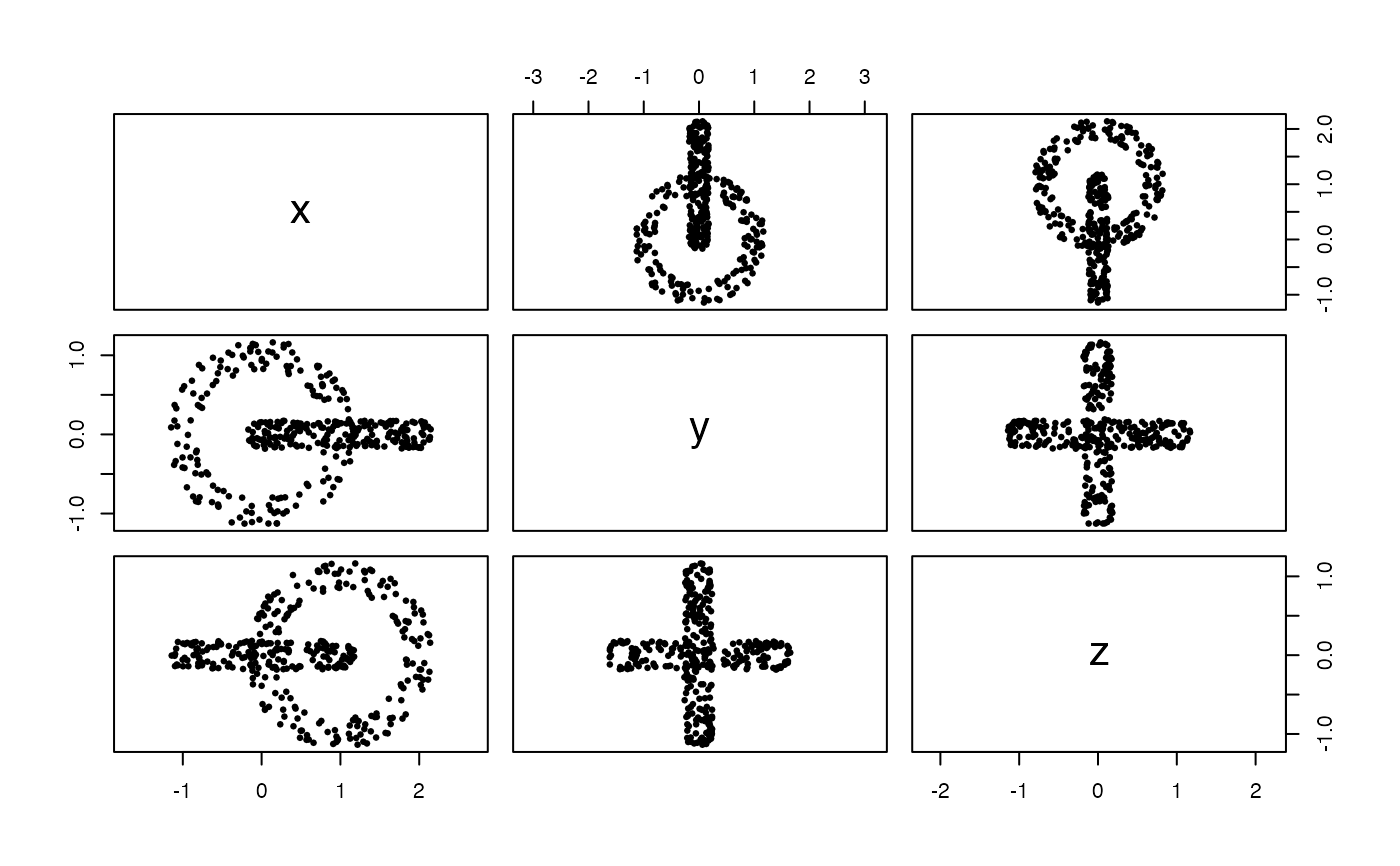
# torus tube embedding in 3-space
x <- sample_torus_tube(120, sd = .05)
pairs(x, asp = 1, pch = 19, cex = .5)
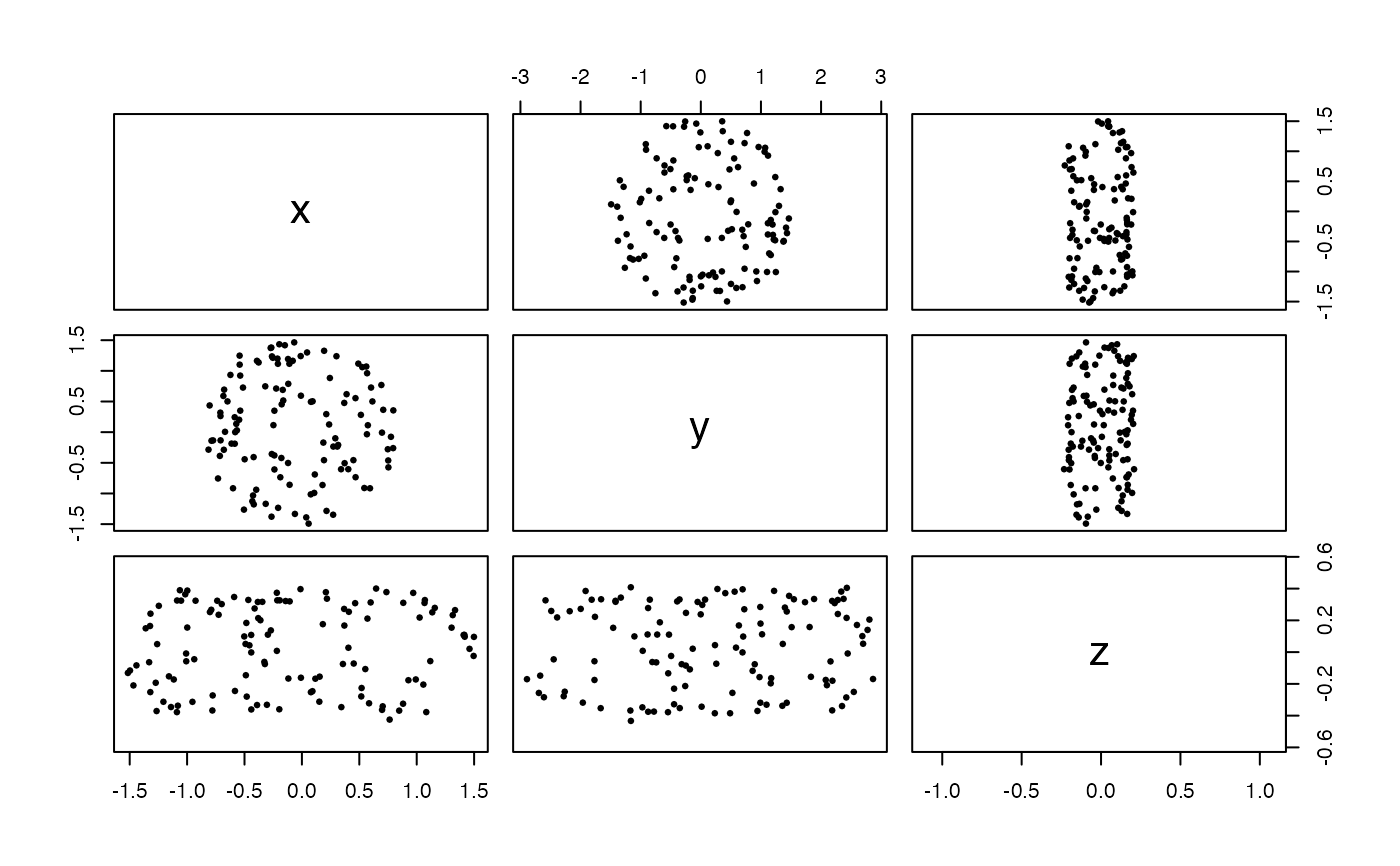 # torus flat embedding in 4-space
x <- sample_torus_flat(120, sd = .05)
pairs(x, asp = 1, pch = 19, cex = .5)
# torus flat embedding in 4-space
x <- sample_torus_flat(120, sd = .05)
pairs(x, asp = 1, pch = 19, cex = .5)
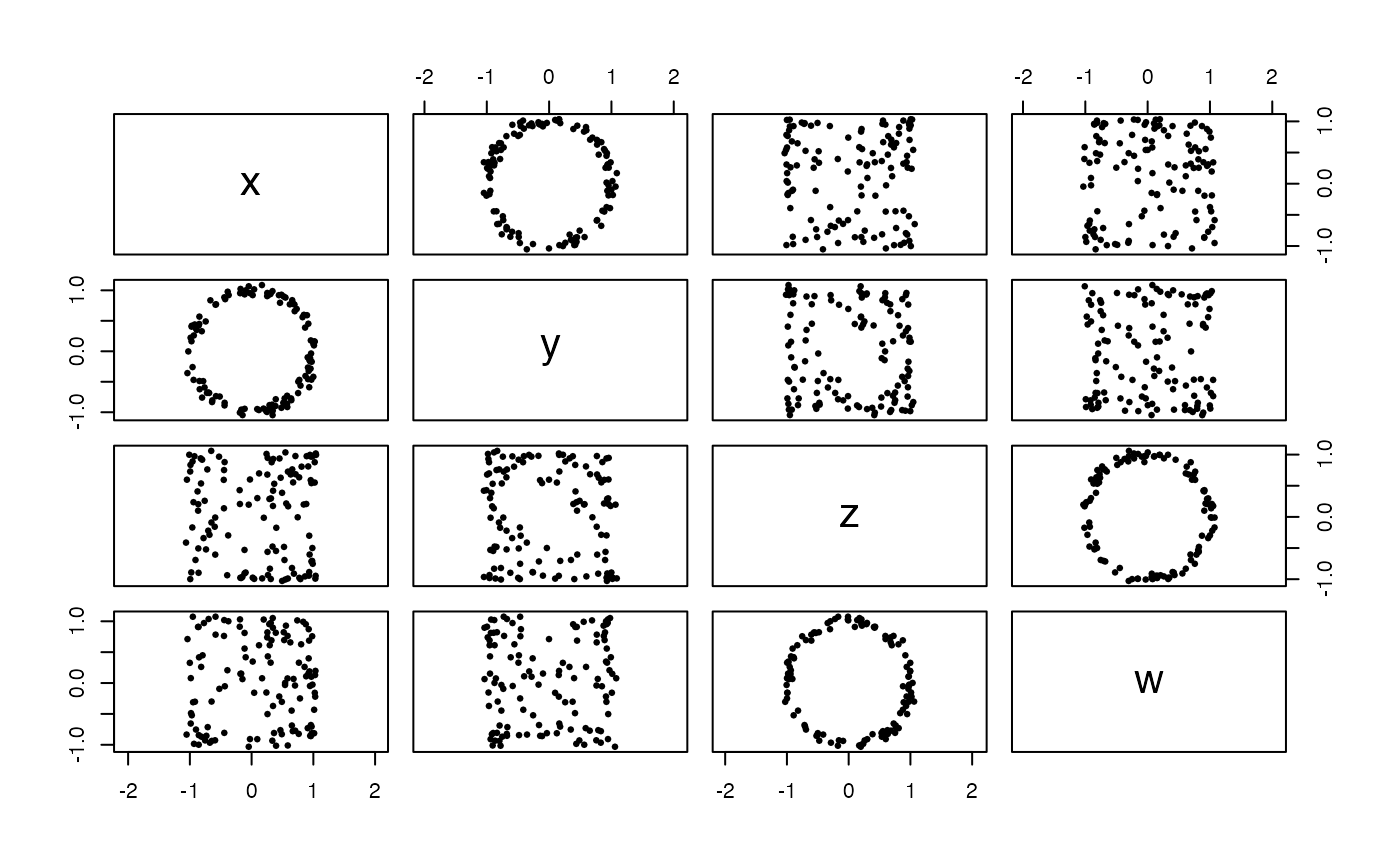 # interlocked tubular tori in 3-space
x <- sample_tori_interlocked(360, ar = 6, sd = .01)
pairs(x, asp = 1, pch = 19, cex = .5)
# interlocked tubular tori in 3-space
x <- sample_tori_interlocked(360, ar = 6, sd = .01)
pairs(x, asp = 1, pch = 19, cex = .5)