Sample (with noise) from Möbius strips

These functions generate uniform samples from Möbius strips in 3-dimensional space, optionally with noise.

sample_mobius_rotoid(n, ar = 2, sd = 0)

Arguments

n

Number of observations.

ar

Aspect ratio for rotoid Möbius surface (ratio of major to minor radii).

sd

Standard deviation of (independent multivariate) Gaussian noise.

Details

The function sample_mobius_rotoid() uses the rotoid Möbius surface parameterization obtained from the now-defunct Encyclopédie des Formes Mathématiques Remarquables. Uniform samples are generated through a rejection sampling process as described by Diaconis, Holmes, and Shahshahani (2013). The Jacobian determinant was symbolically computed and simplified using Mathematica v13.3.1.0.

References

P Diaconis, S Holmes, and M Shahshahani (2013) Sampling from a Manifold. Advances in Modern Statistical Theory and Applications: A Festschrift in honor of Morris L. Eaton, 102--125. doi:10.1214/12-IMSCOLL1006

Examples

set.seed(5898L)

# Möbius strip embedding in 3-space
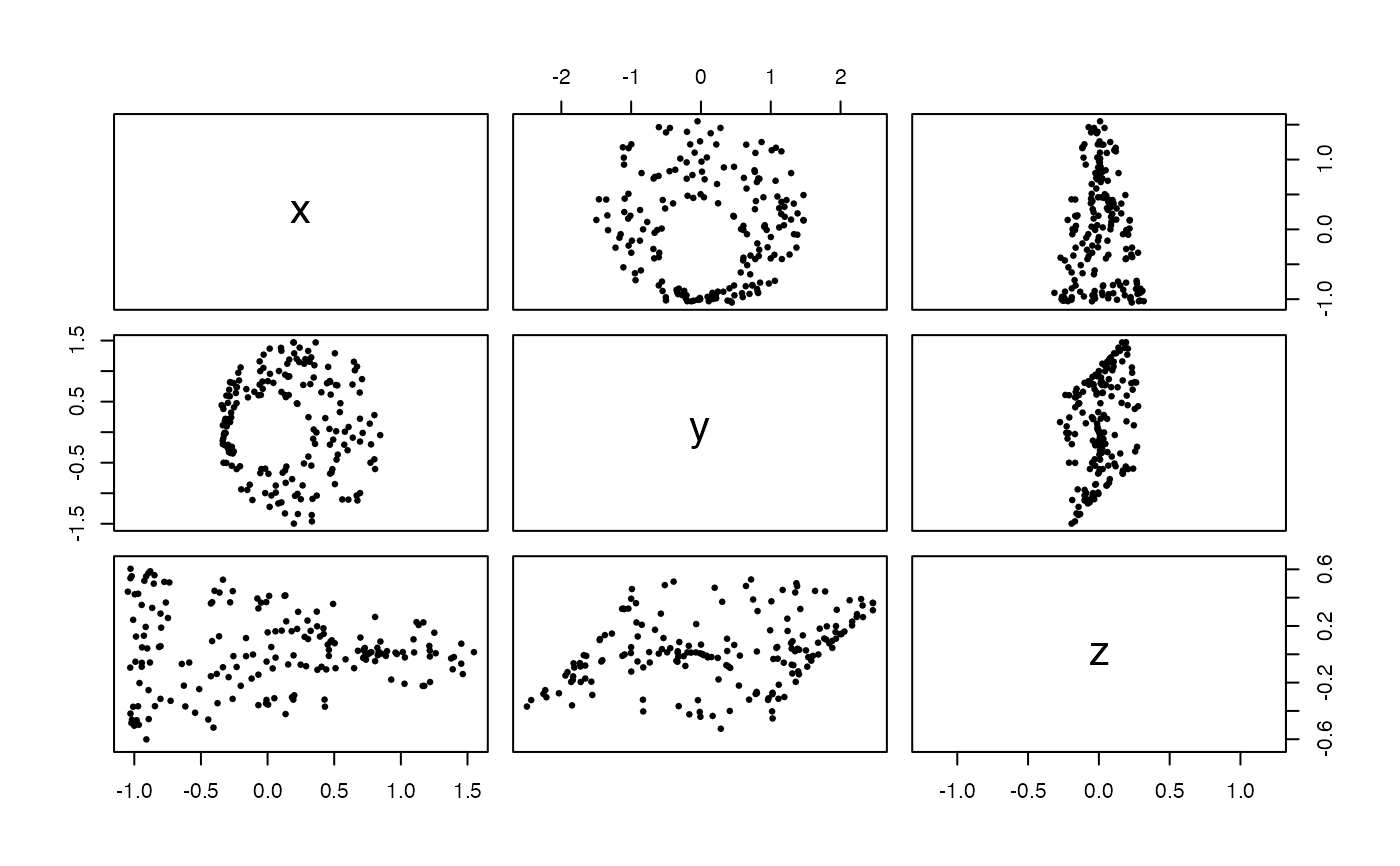
x <- sample_mobius_rotoid(180, ar = 1.5, sd = 0.02)
pairs(x, asp = 1, pch = 19, cex = .5)


# color-code points by coordinates
x_ran <- apply(x, 2L, range)
x_col <- rgb((x[, 1L] - x_ran[1L, 1L]) / (x_ran[2L, 1L] - x_ran[1L, 1L]),
             (x[, 2L] - x_ran[1L, 2L]) / (x_ran[2L, 2L] - x_ran[1L, 2L]),
             (x[, 3L] - x_ran[1L, 3L]) / (x_ran[2L, 3L] - x_ran[1L, 3L]))
pairs(x, asp = 1, pch = 19, cex = .75, col = x_col)


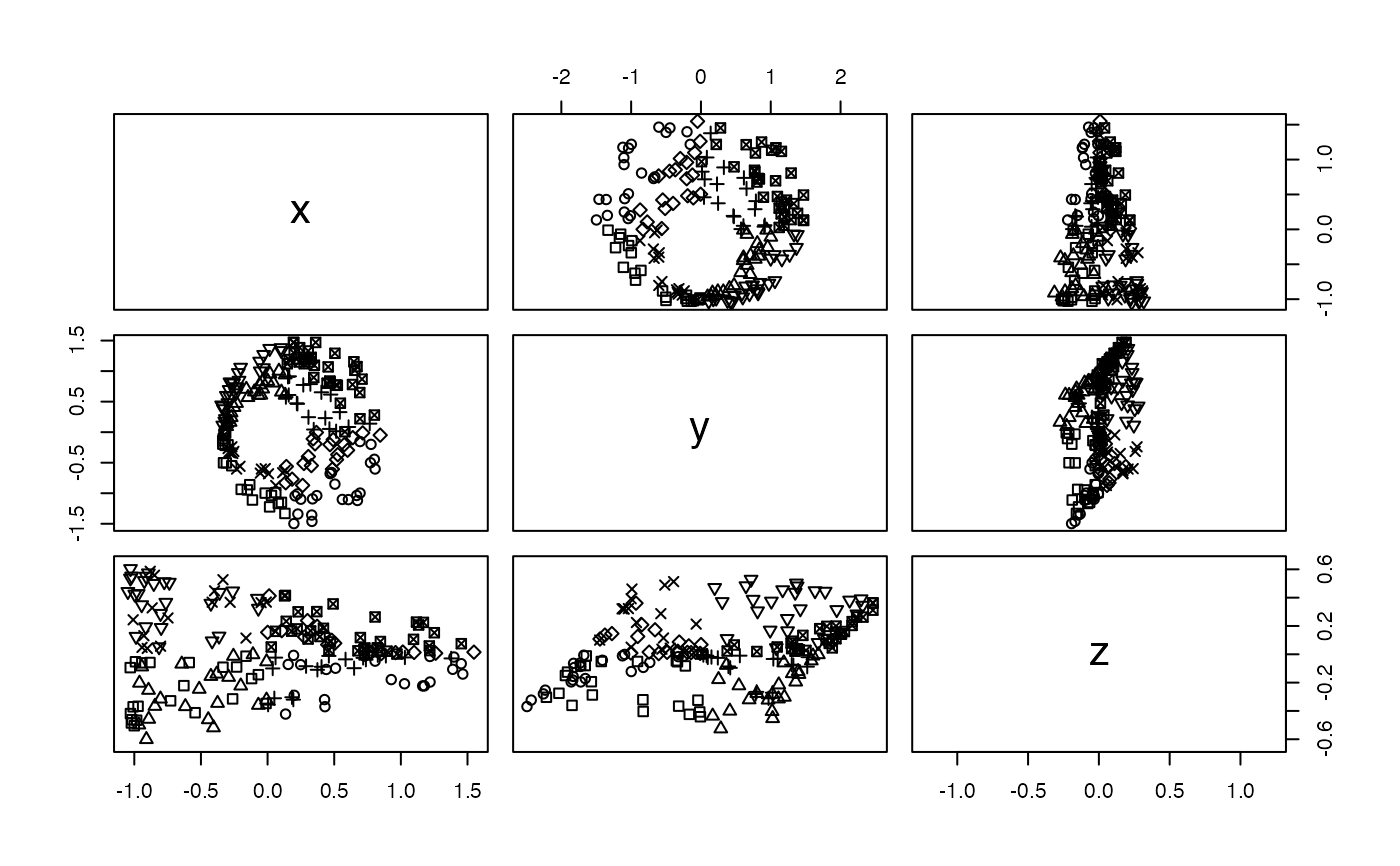
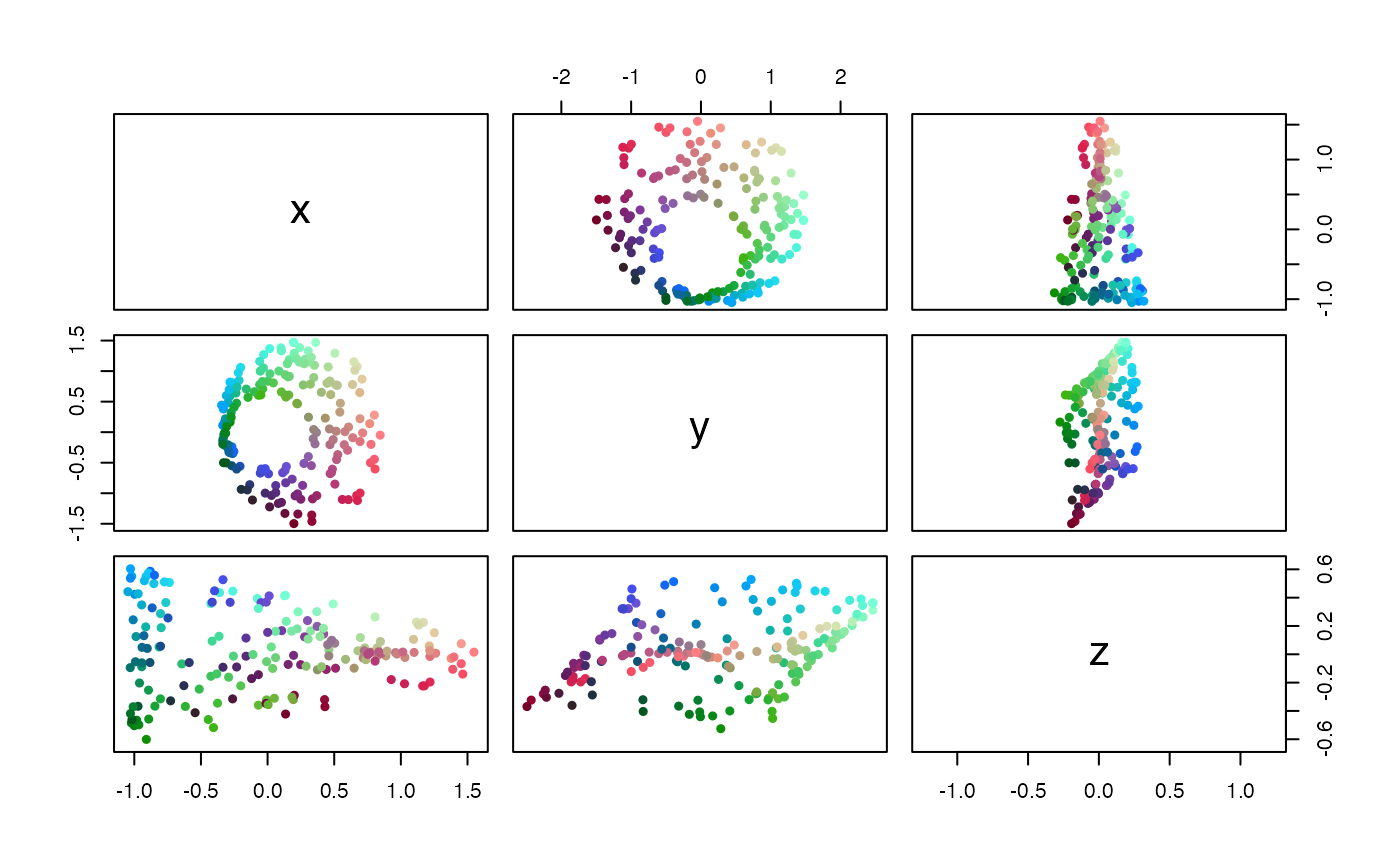# shape-code by octant
x_pch <- apply(x > 0, 1L, \(l) sum(2L ^ seq(0L, 2L) * l))
pairs(x, asp = 1, cex = 1, pch = x_pch)