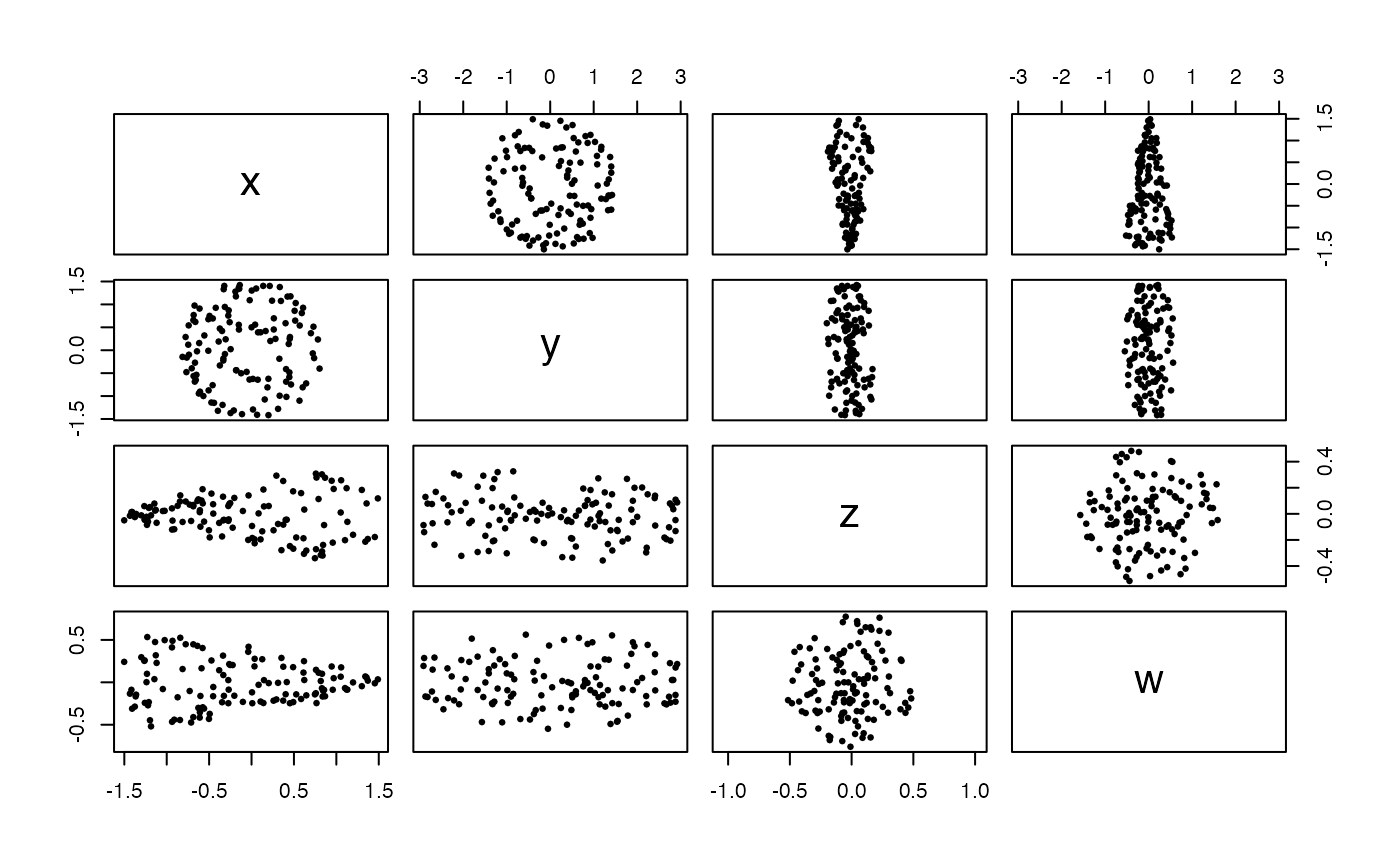
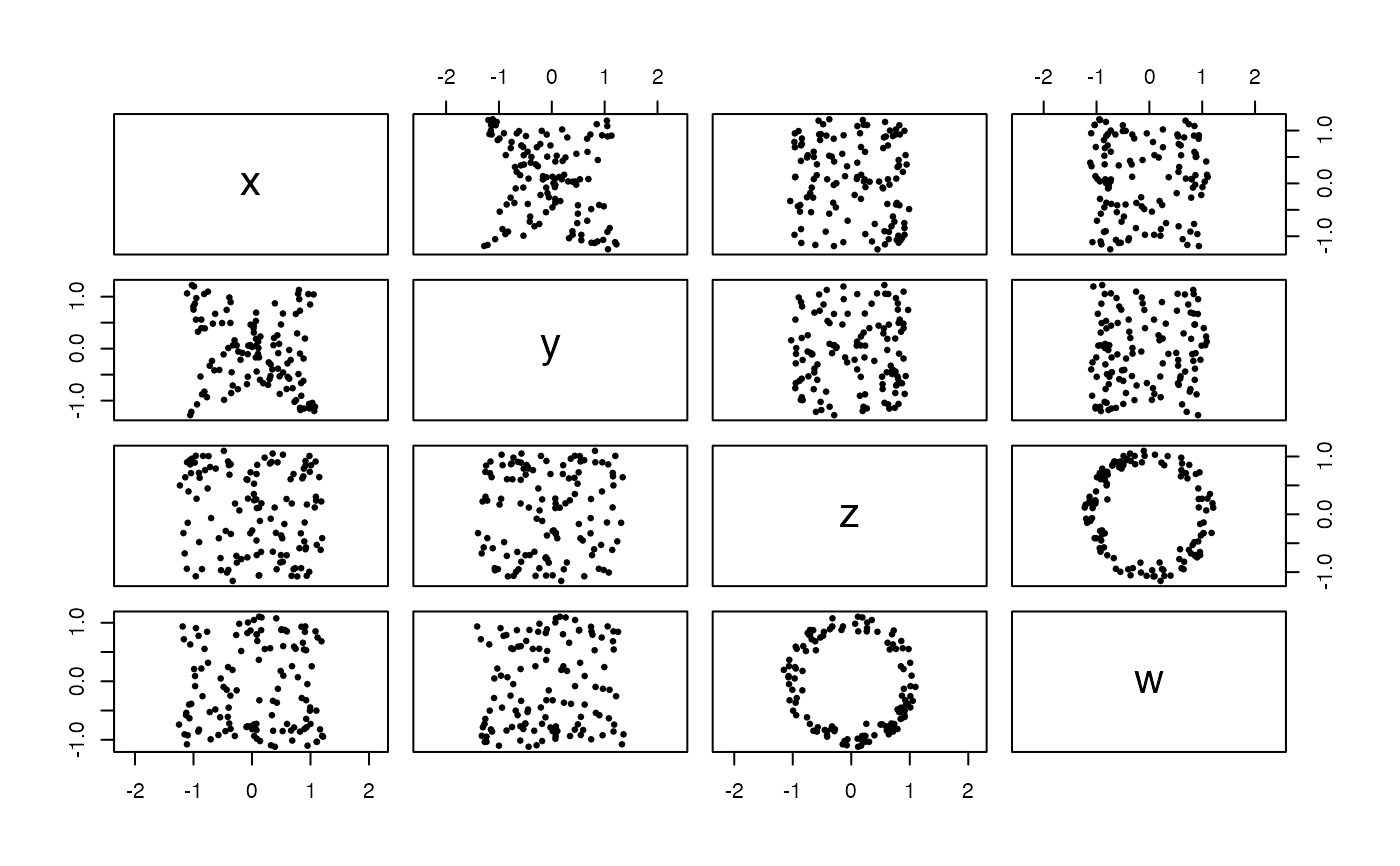
Sample (with noise) from Klein bottles — klein-bottles • tdaunif

These functions generate uniform samples from Klein bottles in 4-dimensional space, optionally with noise.

sample_klein_tube(n, ar = 2, sd = 0)

sample_klein_flat(n, ar = 1, bump = 0.1, sd = 0)

Arguments

n: Number of observations.
ar: Aspect ratio for Möbius tube Klein bottle (ratio of major and minor radii) or flat torus-based Klein bottle (ratio of scale factors).
sd: Standard deviation of (independent multivariate) Gaussian noise.
bump: Bump constant for the flat torus-based Klein bottle.

Details

The function sample_klein_tube() uses the Möbius tube parameterization obtained from the now-defunct Encyclopédie des Formes Mathématiques Remarquables and currently documented on Wikipedia.

The function sample_klein_flat() uses a flat parameterization based on that of the torus, as presented on Wikipedia.

Both uniform samples are generated through a rejection sampling process as described by Diaconis, Holmes, and Shahshahani (2013).

References

P Diaconis, S Holmes, and M Shahshahani (2013) Sampling from a Manifold. Advances in Modern Statistical Theory and Applications: A Festschrift in honor of Morris L. Eaton, 102--125. doi:10.1214/12-IMSCOLL1006

Examples

set.seed(834L)

# Klein bottle tube embedding in 4-space
x <- sample_klein_tube(120, sd = .05)
pairs(x, asp = 1, pch = 19, cex = .5)


# Klein bottle flat torus-based embedding in 4-space
x <- sample_klein_flat(120, sd = .05)
pairs(x, asp = 1, pch = 19, cex = .5)