Sample (with noise) from archimedean spirals and swiss rolls
Source:R/archimedean-spirals.r
arch-spirals.RdThese functions generate uniform samples from archimedean spirals in 2-dimensional space or from swiss rolls in 3-dimensional space, optionally with noise.
sample_arch_spiral(n, ar = 1, arms = 1L, min_wrap = 0, max_wrap = 1, sd = 0)
sample_swiss_roll(
n,
ar = 1,
arms = 1L,
min_wrap = 0,
max_wrap = 1,
width = 2 * pi,
sd = 0
)Arguments
- n
Number of observations.
- ar
Aspect ratio of spiral (ratio of width/height)
- arms
Number of spiral arms.
- min_wrap
The wrap of the spiral from which sampling begins.
- max_wrap
The wrap of the spiral at which sampling ends.
- sd
Standard deviation of (independent multivariate) Gaussian noise.
- width
Width of the swiss roll (with respect to the radius of the spiral at one wrap).
Details
The archimedean spiral starts at the origin and wraps around itself such that radial distances between all the spiral branches are equal. The specific parameterization was taken from Koeller (2002). The uniform sample is generated through a rejection sampling process as described by Diaconis, Holmes, and Shahshahani (2013).
The swiss roll sampler is patterned after one in drtoolbox and extended from the archimedean spiral sampler.
References
Koeller, J. (2002). Spirals. Retrieved July 18, 2019, from http://www.mathematische-basteleien.de/spiral.htm
P Diaconis, S Holmes, and M Shahshahani (2013) Sampling from a Manifold. Advances in Modern Statistical Theory and Applications: A Festschrift in honor of Morris L. Eaton, 102--125. doi:10.1214/12-IMSCOLL1006
Examples
set.seed(77151L)
#Uniformly sampled archimedean spiral in 2-space, with 1 wrap
x <- sample_arch_spiral(360, min_wrap = 0, max_wrap = 1)
plot(x, asp = 1, pch = 19, cex = .5)
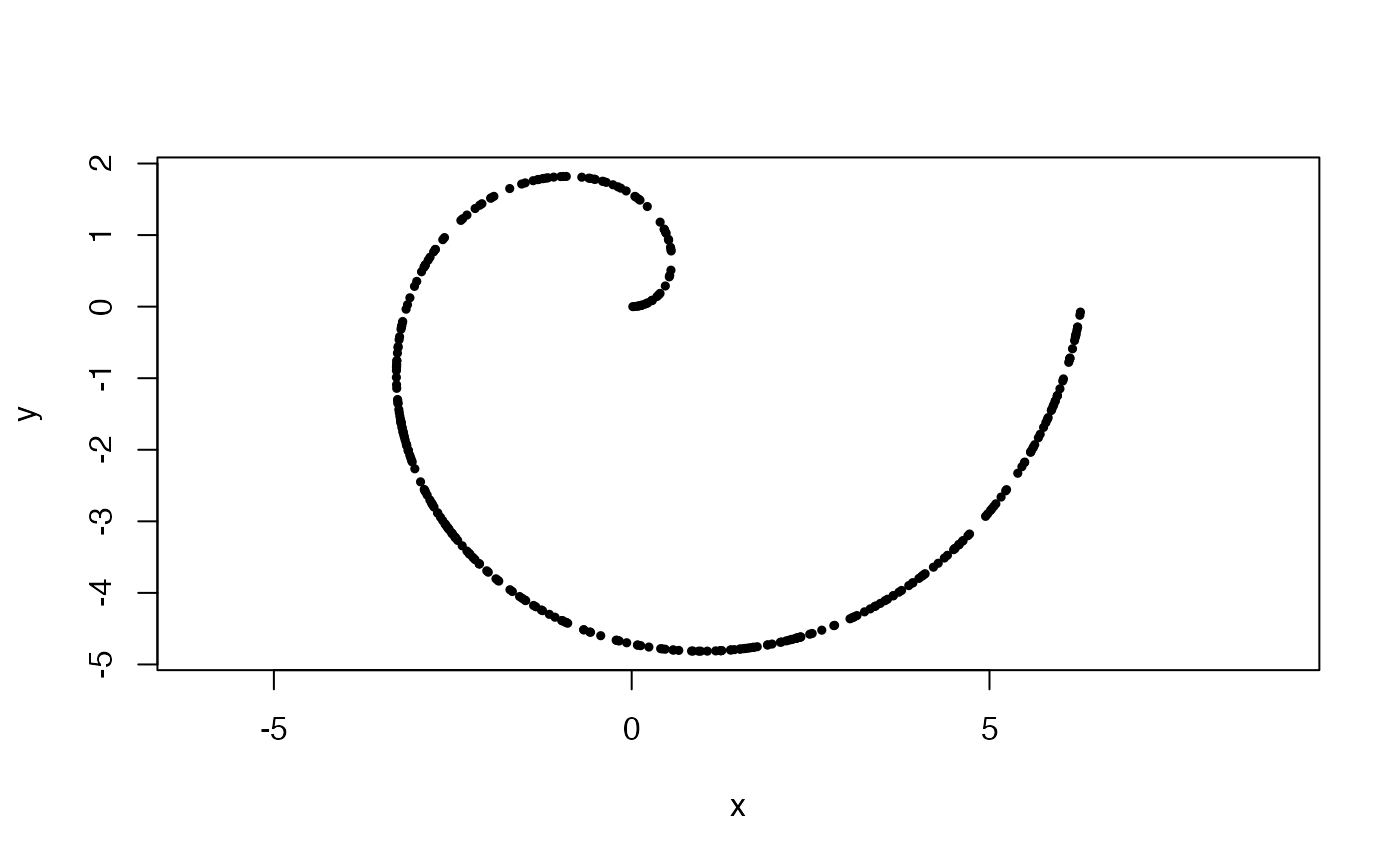 #Uniformly sampled archimedean spiral in 2-space, with 1 wrap
#and aspect ratio of 2:1
x <- sample_arch_spiral(360, ar = 2, min_wrap = 0, max_wrap = 1)
plot(x, asp = 1, pch = 19, cex = .5)
#Uniformly sampled archimedean spiral in 2-space, with 1 wrap
#and aspect ratio of 2:1
x <- sample_arch_spiral(360, ar = 2, min_wrap = 0, max_wrap = 1)
plot(x, asp = 1, pch = 19, cex = .5)
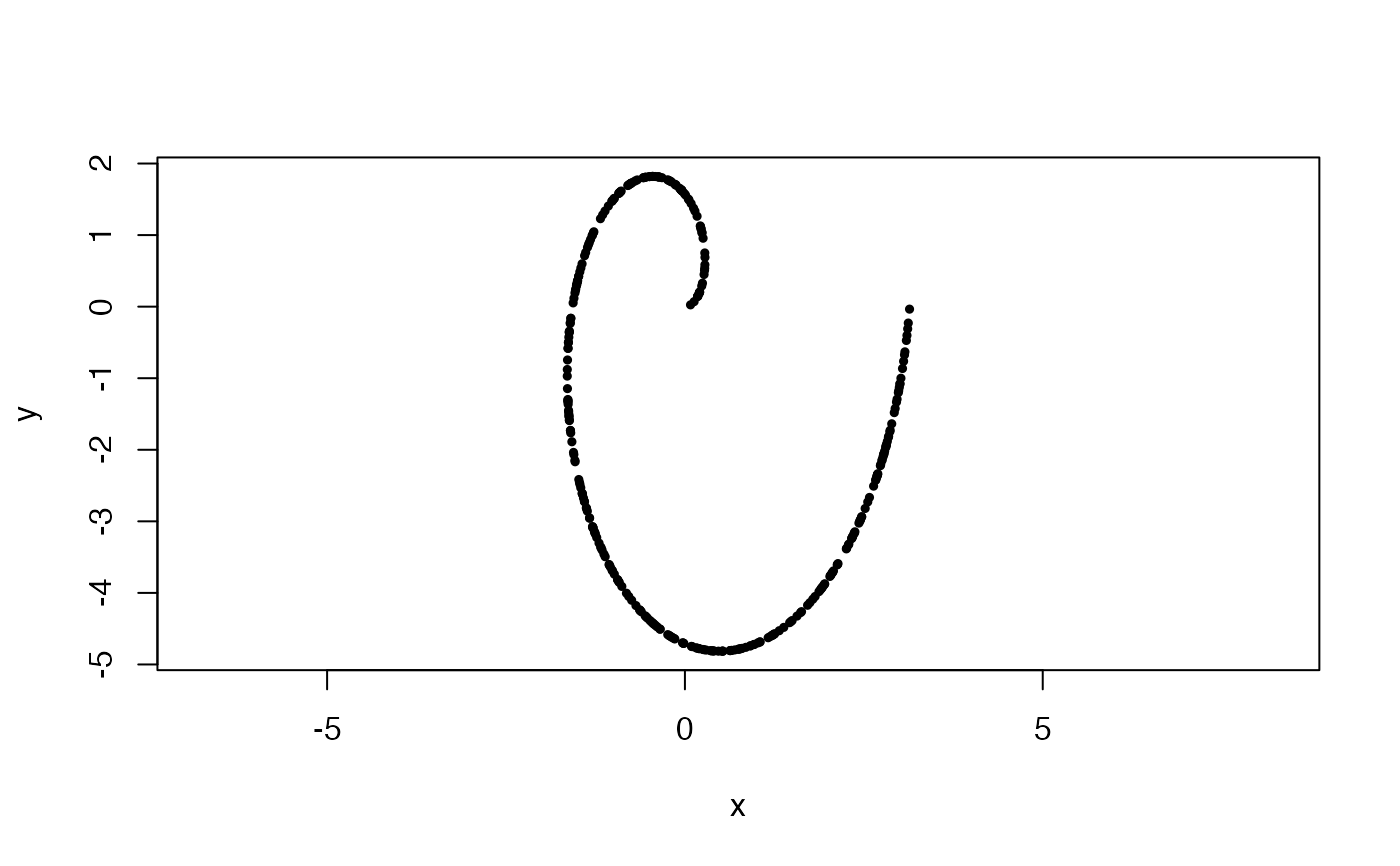
 #Uniformly sampled archimedean spiral in 2-space, with 1 wrap
#and aspect ratio of 1:2
x <- sample_arch_spiral(360, ar = 0.5, min_wrap = 0, max_wrap = 1)
plot(x, asp = 1, pch = 19, cex = .5)
#Uniformly sampled archimedean spiral in 2-space, with 1 wrap
#and aspect ratio of 1:2
x <- sample_arch_spiral(360, ar = 0.5, min_wrap = 0, max_wrap = 1)
plot(x, asp = 1, pch = 19, cex = .5)
 #Uniformly sampled archimedean spiral in 2-space, with 5 wraps
x <- sample_arch_spiral(360, min_wrap = 0, max_wrap = 5)
plot(x, asp = 1, pch = 19, cex = .5)
#Uniformly sampled archimedean spiral in 2-space, with 5 wraps
x <- sample_arch_spiral(360, min_wrap = 0, max_wrap = 5)
plot(x, asp = 1, pch = 19, cex = .5)
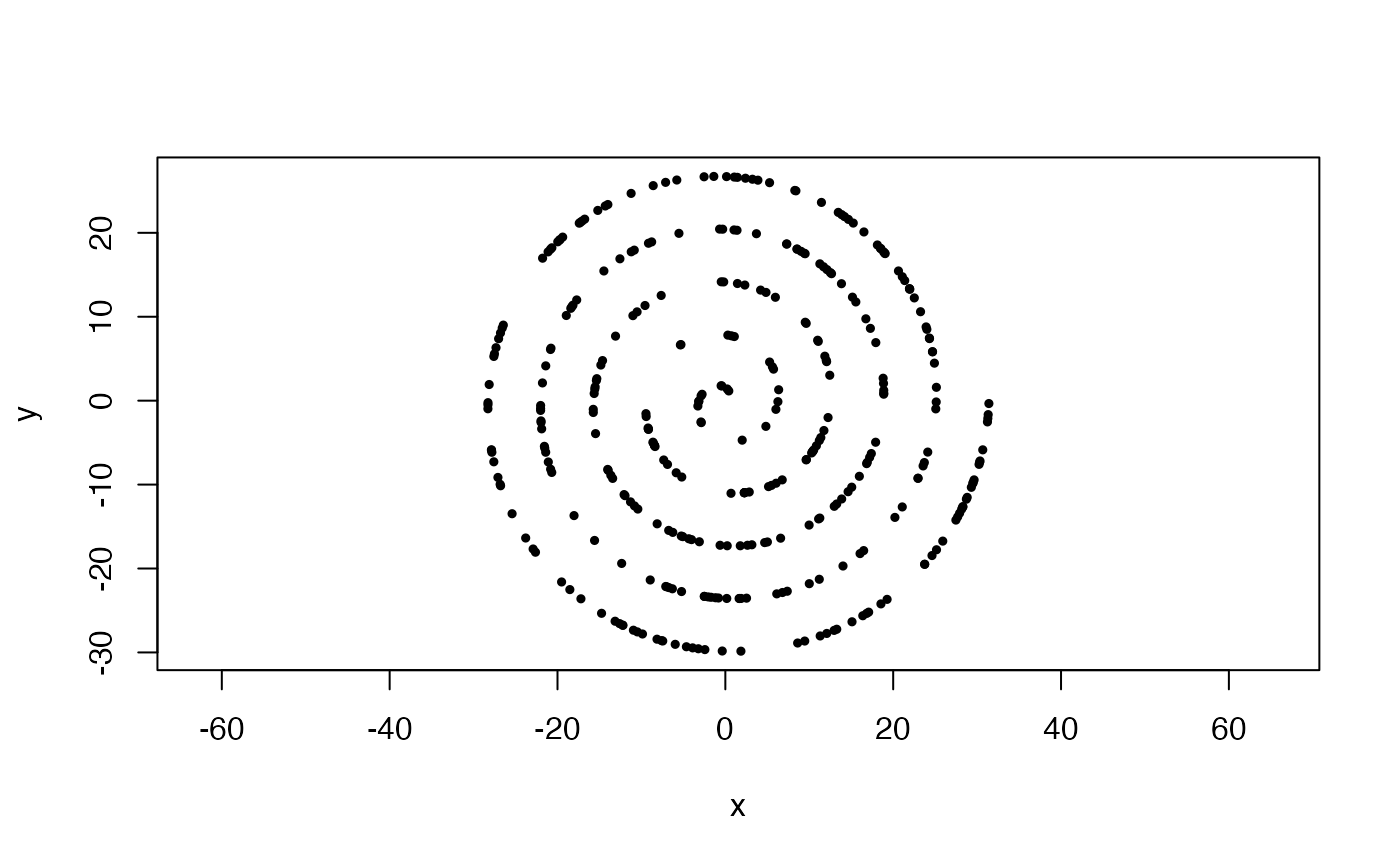 #Uniformly sampled archimedean spiral in 2-space, with 5 wraps and starting from
#2 wraps
x <- sample_arch_spiral(360, min_wrap = 2, max_wrap = 5)
plot(x, asp = 1, pch = 19, cex = .5)
#Uniformly sampled archimedean spiral in 2-space, with 5 wraps and starting from
#2 wraps
x <- sample_arch_spiral(360, min_wrap = 2, max_wrap = 5)
plot(x, asp = 1, pch = 19, cex = .5)
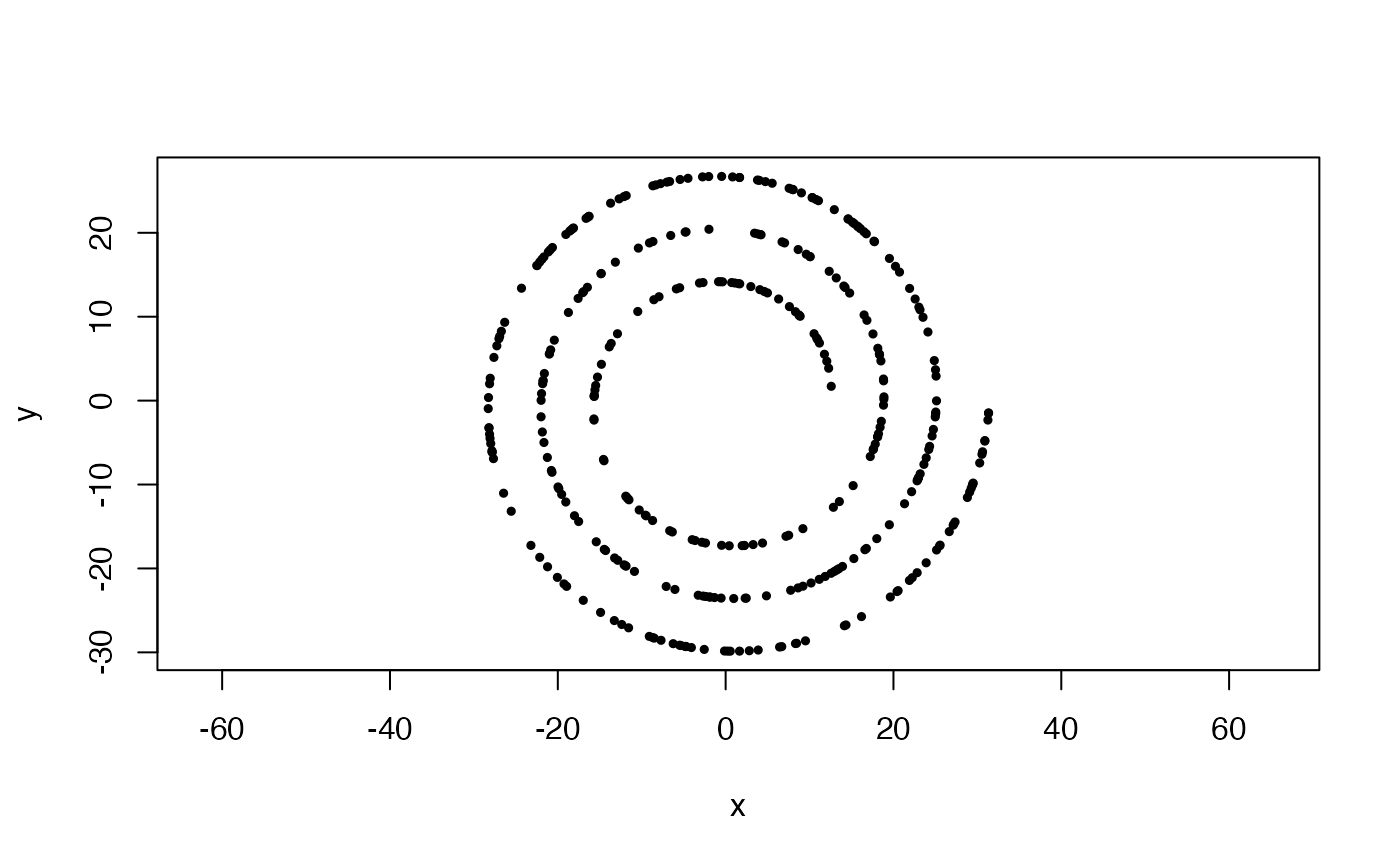 #Uniformly sampled archimedean spiral, from 1 to 2 wraps, with 3 arms
x <- sample_arch_spiral(360, arms = 3, min_wrap = 1, max_wrap = 2)
plot(x, asp = 1, pch = 19, cex = .5)
#Uniformly sampled archimedean spiral, from 1 to 2 wraps, with 3 arms
x <- sample_arch_spiral(360, arms = 3, min_wrap = 1, max_wrap = 2)
plot(x, asp = 1, pch = 19, cex = .5)
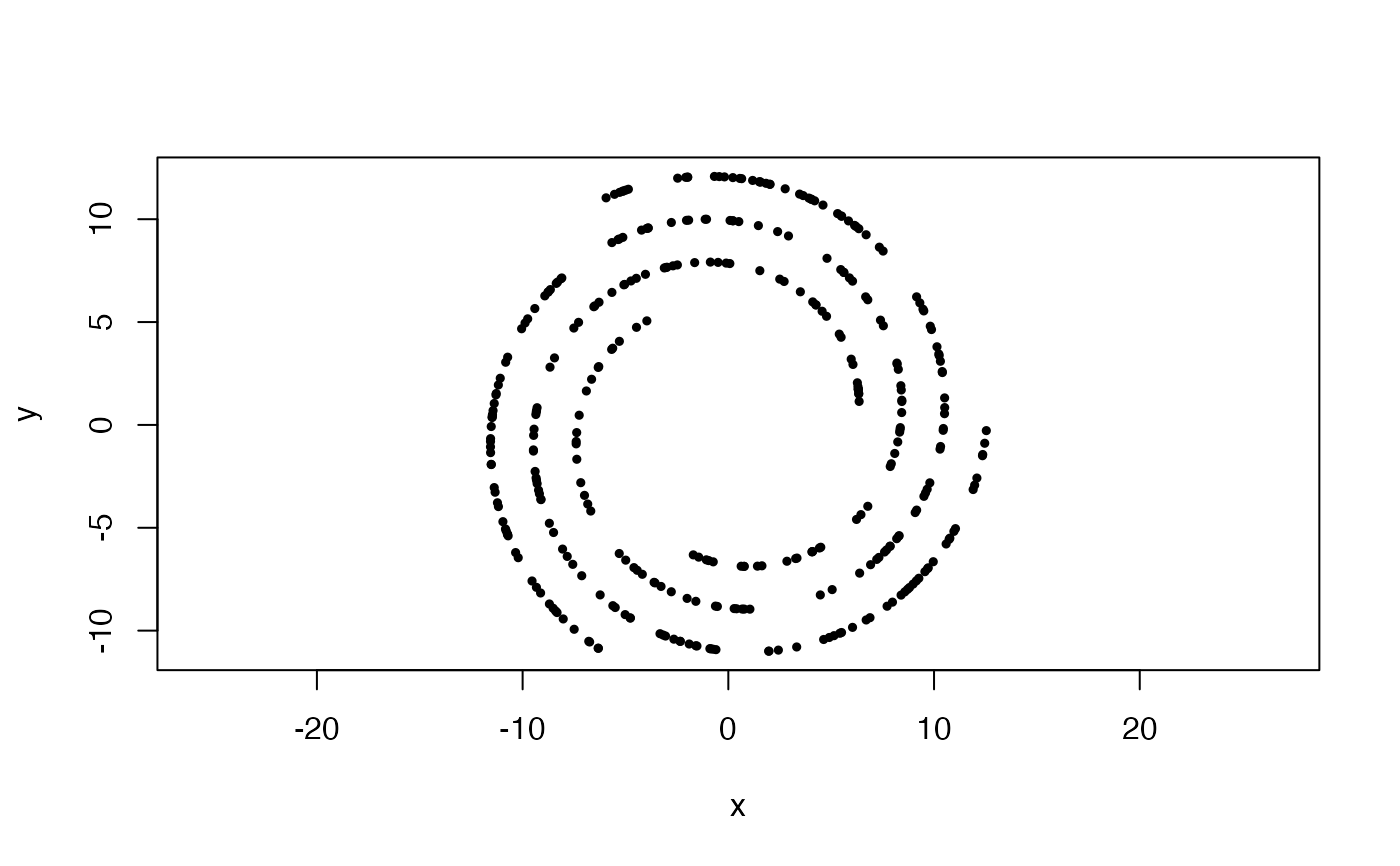 #Uniformly sampled archimedean spiral in 2-space, with 1 wrap and noise with a
#standard deviation of 0.1
x <- sample_arch_spiral(360, min_wrap = 0, max_wrap = 1, sd = 0.1)
plot(x, asp = 1, pch = 19, cex = .5)
#Uniformly sampled archimedean spiral in 2-space, with 1 wrap and noise with a
#standard deviation of 0.1
x <- sample_arch_spiral(360, min_wrap = 0, max_wrap = 1, sd = 0.1)
plot(x, asp = 1, pch = 19, cex = .5)
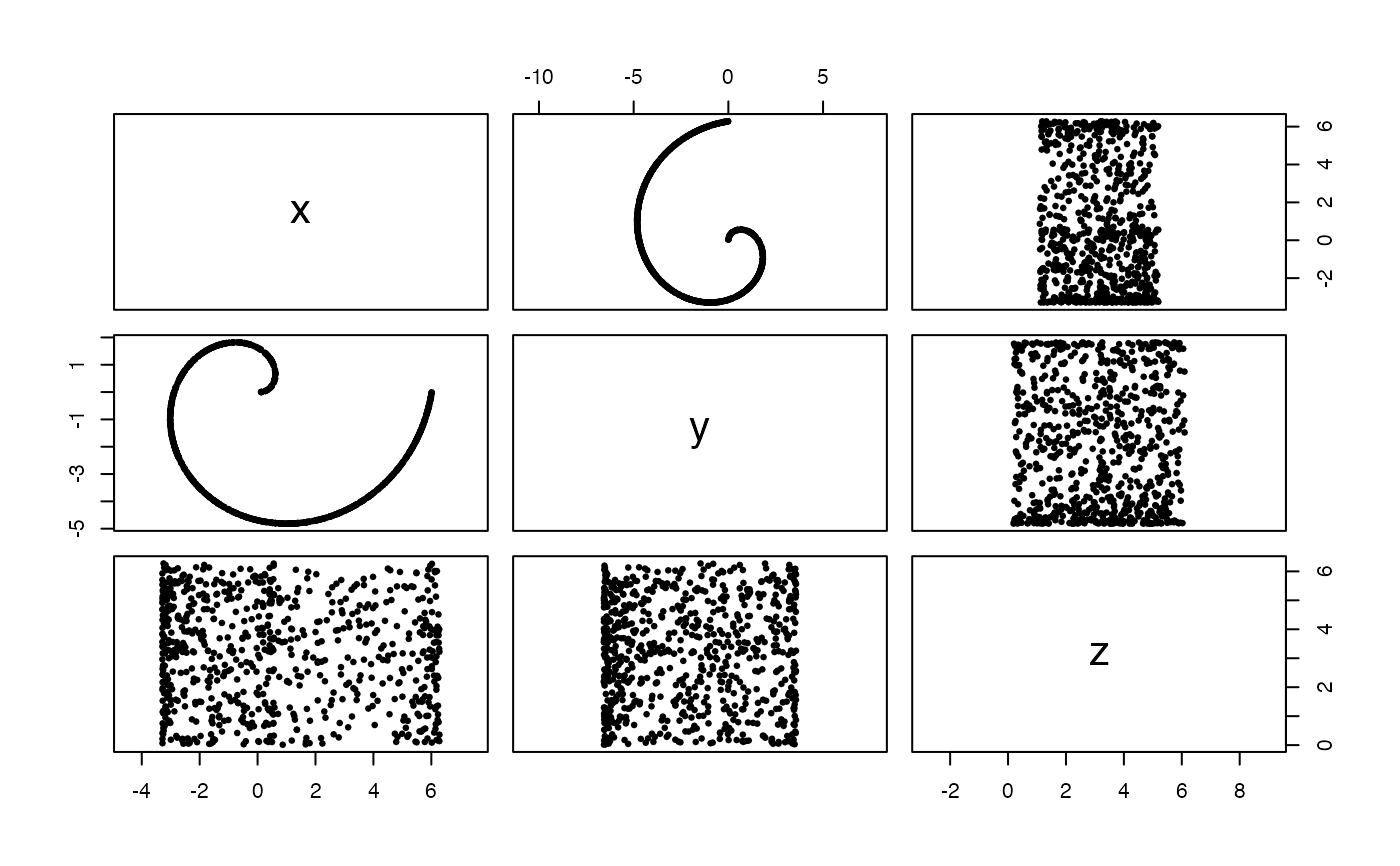
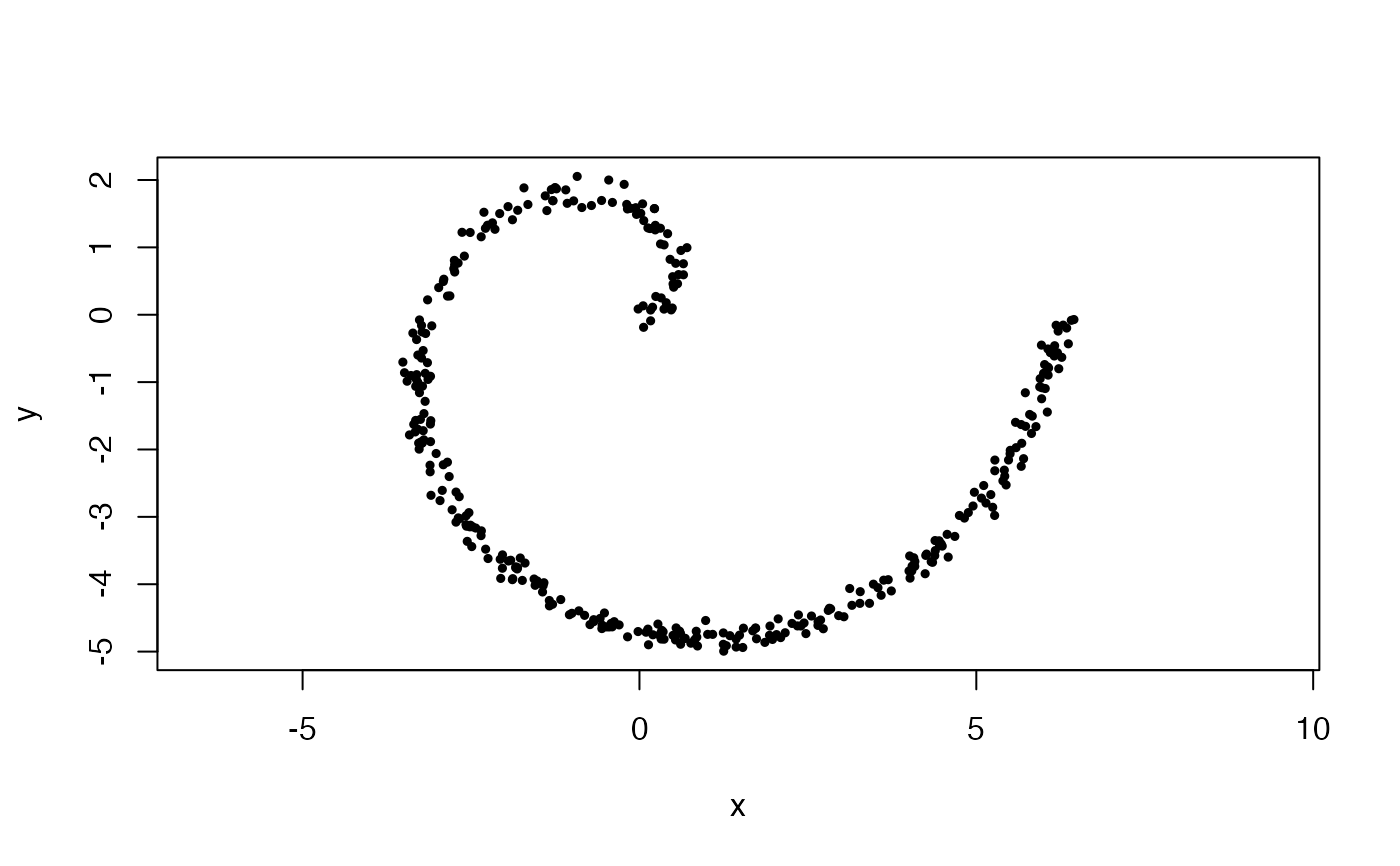 #Uniformly sampled swiss roll in 3-space, from 0 to 1 wraps and width 2*pi
x <- sample_swiss_roll(720, width = 2*pi)
pairs(x, asp = 1, pch = 19, cex = .5)
#Uniformly sampled swiss roll in 3-space, from 0 to 1 wraps and width 2*pi
x <- sample_swiss_roll(720, width = 2*pi)
pairs(x, asp = 1, pch = 19, cex = .5)
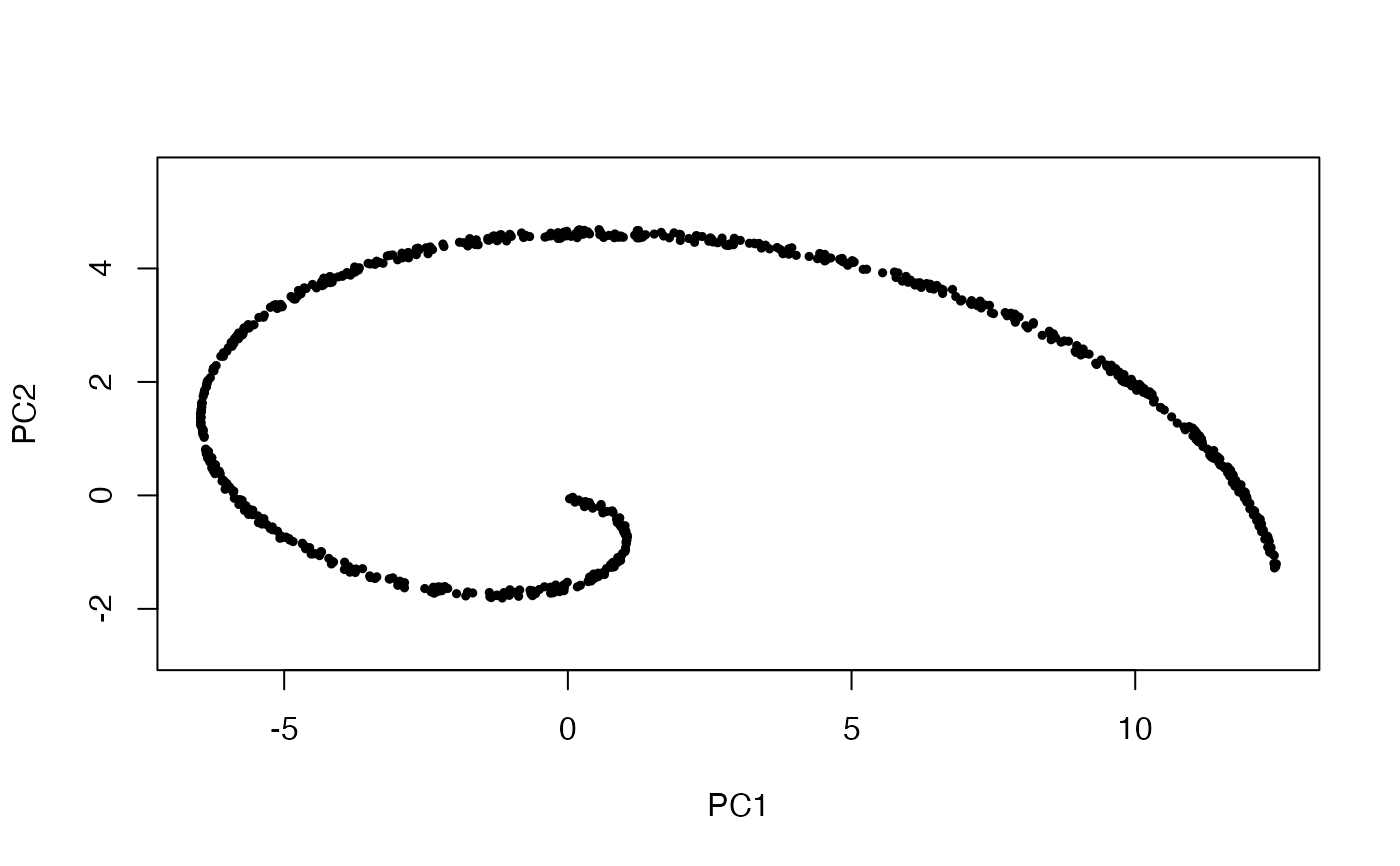
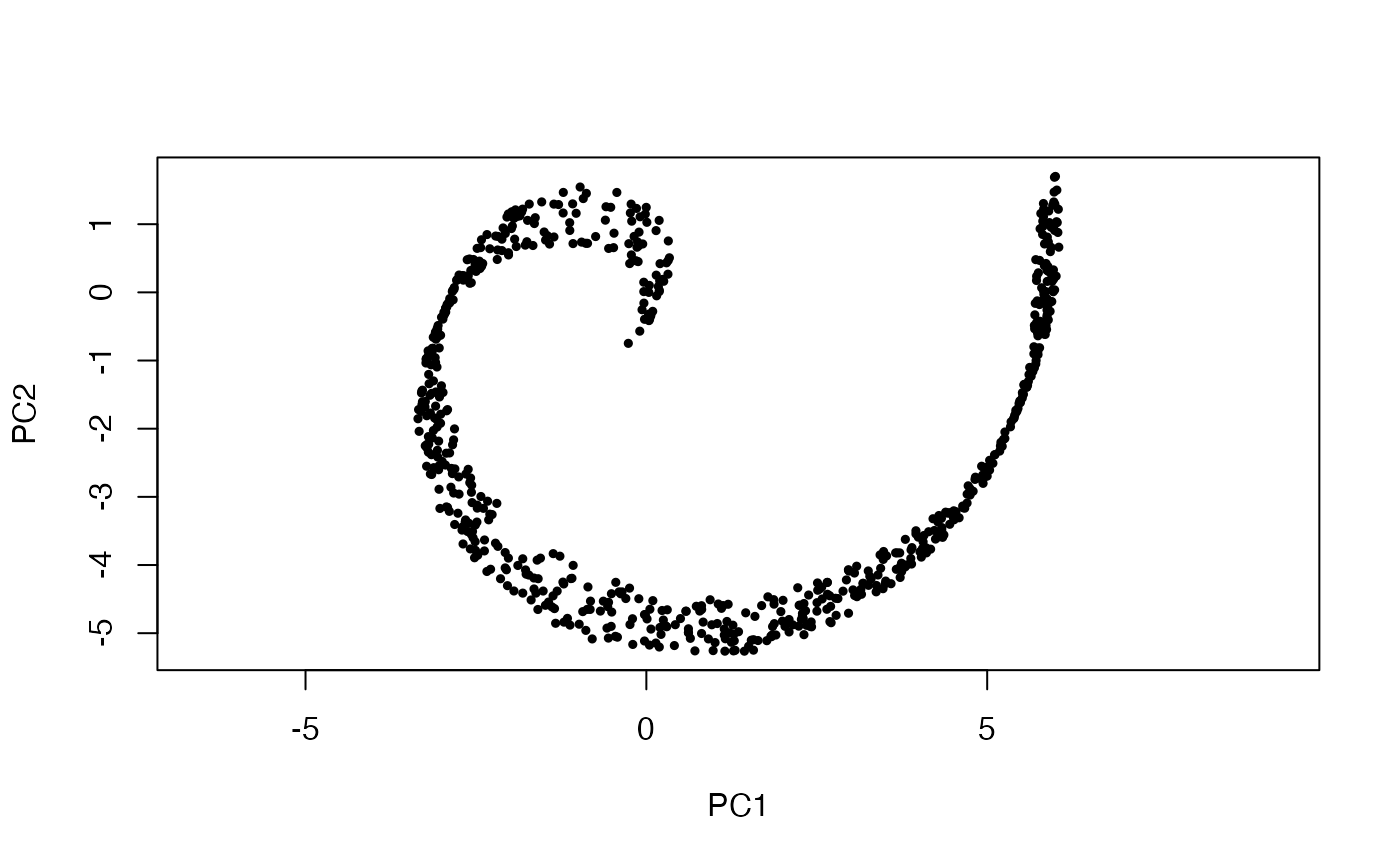
 pca <- prcomp(x)
plot(x %*% pca$rotation, asp = 1, pch = 19, cex = .5)
pca <- prcomp(x)
plot(x %*% pca$rotation, asp = 1, pch = 19, cex = .5)
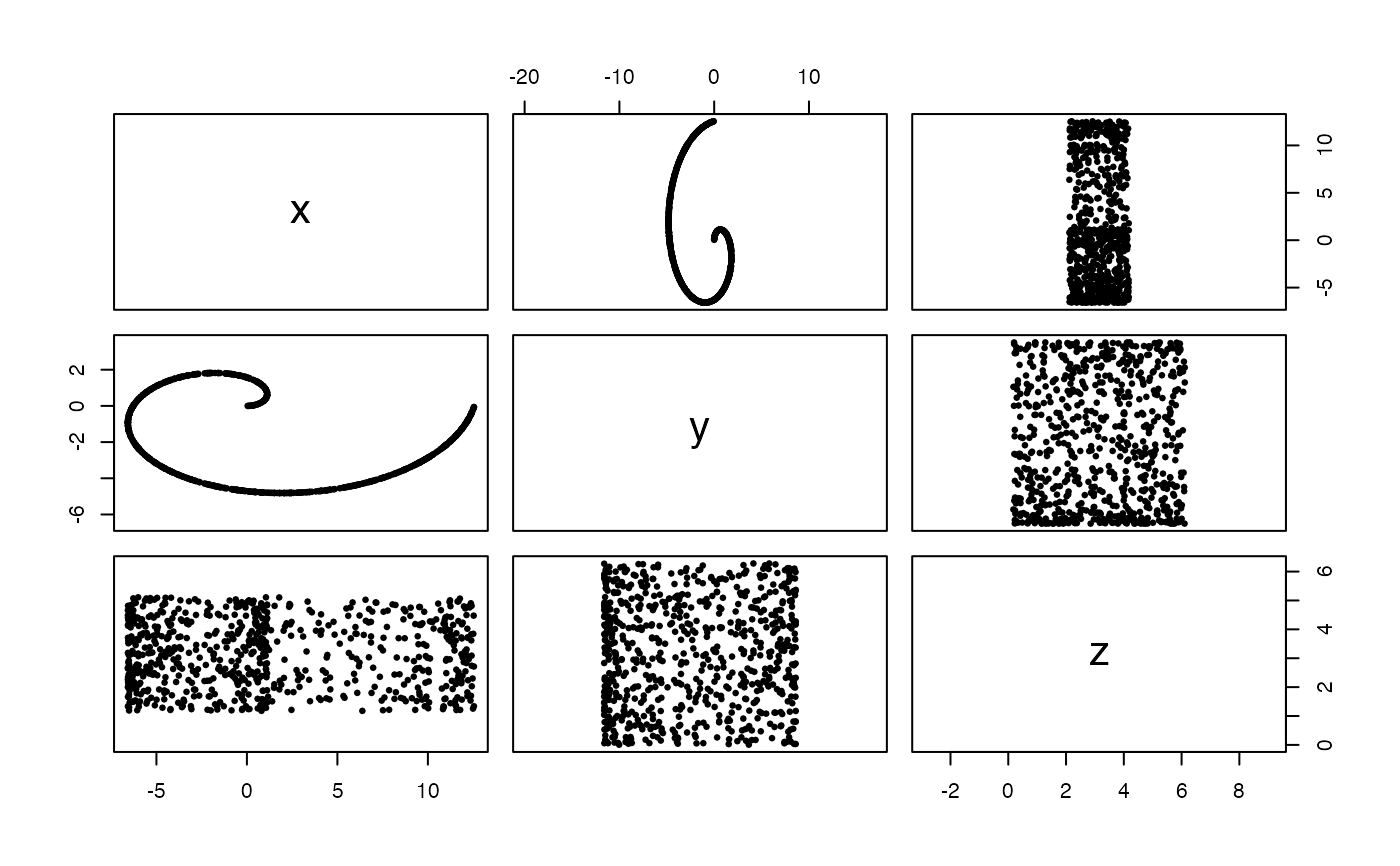
 #Uniformly sampled swiss roll in 3-space, from 0 to 1 wraps and width 2*pi
x <- sample_swiss_roll(720, ar = 2, width = 2*pi)
pairs(x, asp = 1, pch = 19, cex = .5)
#Uniformly sampled swiss roll in 3-space, from 0 to 1 wraps and width 2*pi
x <- sample_swiss_roll(720, ar = 2, width = 2*pi)
pairs(x, asp = 1, pch = 19, cex = .5)
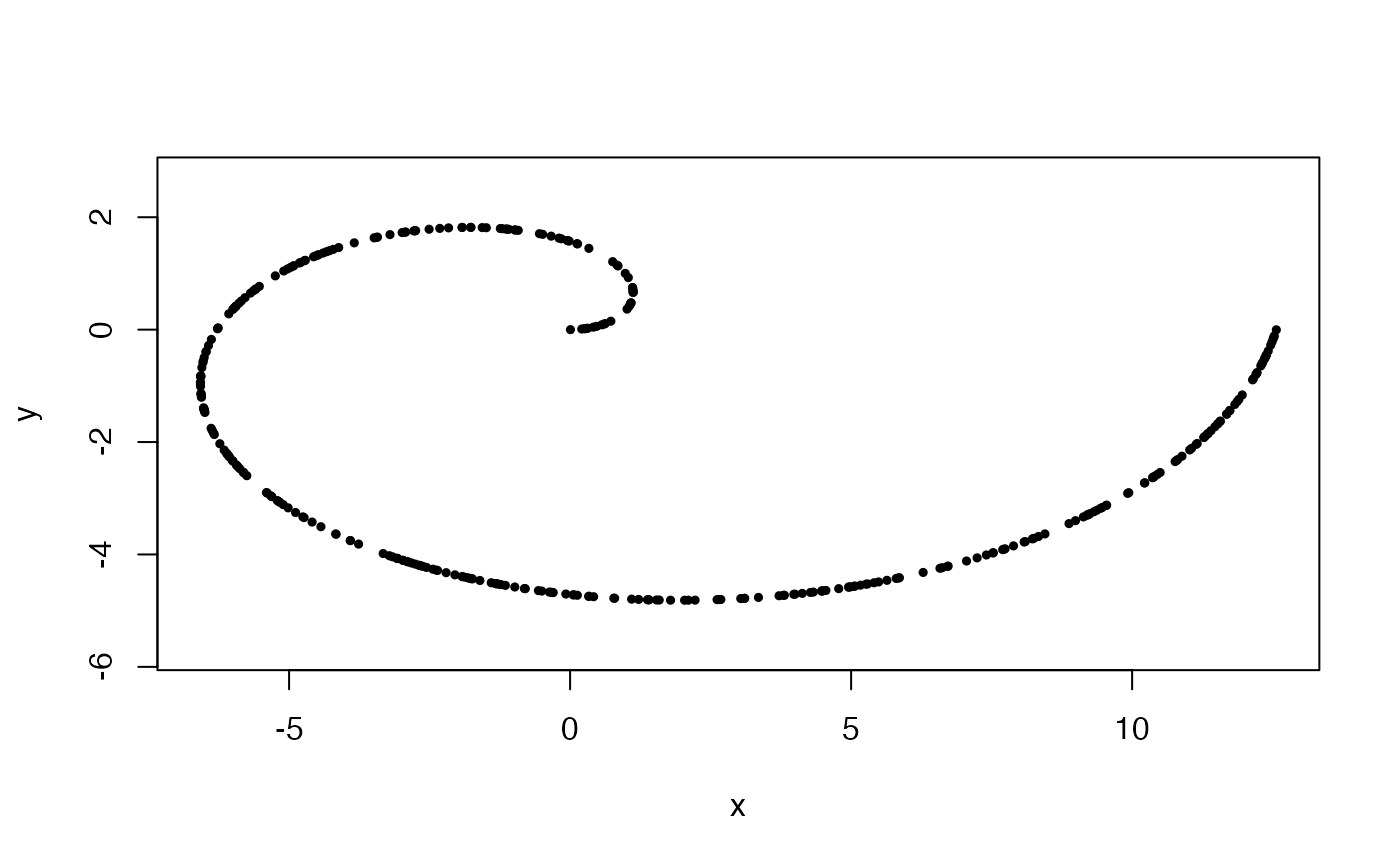
 pca <- prcomp(x)
plot(x %*% pca$rotation, asp = 1, pch = 19, cex = .5)
pca <- prcomp(x)
plot(x %*% pca$rotation, asp = 1, pch = 19, cex = .5)